TOÁN CHO CÁC NHÀ KINH TẾ NEU| TÓM TẮT KIẾN THỨC GIỚI HẠN CỦA HÀM SỐ
Ngày: 27/12/2023
TOÁN CHO CÁC NHÀ KINH TẾ NEU
GIỚI HẠN CỦA HÀM SỐ
Giới hạn của hàm số là nội dung quan trọng nhất trong chương học mở đầu của môn Toán cho các nhà kinh tế được giảng dạy tại NEU. Bài học ngay hôm nay tập trung tìm hiểu về khái niệm giới hạn và các tính chất tổng quát của giới hạn, tính giới hạn bằng các kỹ thuật khác nhau và tìm hiểu các giới hạn liên quan đến vô hạn. Bài viết là tổng hợp những kiến thức trọng tâm sẽ xuất hiện trong đề thi môn học này tại NEU, do vậy các bạn sinh viên hãy đọc thật kĩ nhé !
1. Giới thiệu trực quan về giới hạn
Giả sử giám đốc một công ty bất động sản xác định được rằng, 𝑡 năm sau kể từ bây giờ, sẽ có khoảng 𝑆 căn hộ ở một địa phương bán được, trong đó𝑆(𝑡)=(−2𝑡3+19𝑡2−8𝑡−9)/(−𝑡2+8𝑡−7)
Hỏi doanh số sau một năm dự kiến bằng bao nhiêu?Phân tích

Kết luận: “𝑆(𝑡) có giá trị giới hạn bằng 4 khi 𝑡 tiến đến 1”, ta viết:
limS(t)(𝑡→1)=4
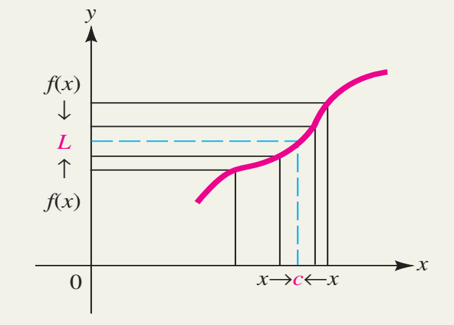
Định nghĩa:
Nếu 𝑓(𝑥) ngày càng gần tới số 𝐿 khi 𝑥 ngày càng gần tới 𝑐 từ cả hai phía thì số 𝐿 được gọi là giới hạn của hàm 𝑓(𝑥) khi 𝑥 tiến gần đến 𝑐.Ký hiệu: lim f(x)(𝑥→𝑐) =𝐿
Ví dụ: Ước lượng giới hạn bằng cách lập bảng
Sử dụng bảng giá trị để ước lượng giới hạn sau:
lim(𝑥→1)[(√𝑥−1)/(𝑥−1)〗
Một số lưu ý:
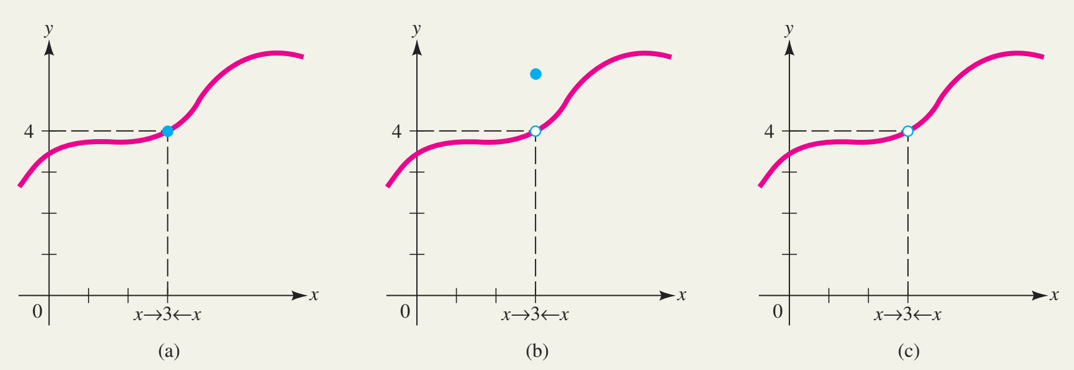
♦ Giới hạn mô tả hành vi của hàm số gần một điểm cụ thể, không nhất thiết phải tại chính điểm đó.
♦ Dưới đây là VD về 3 hàm đều thỏa mãn limf(x)(x→3)=4
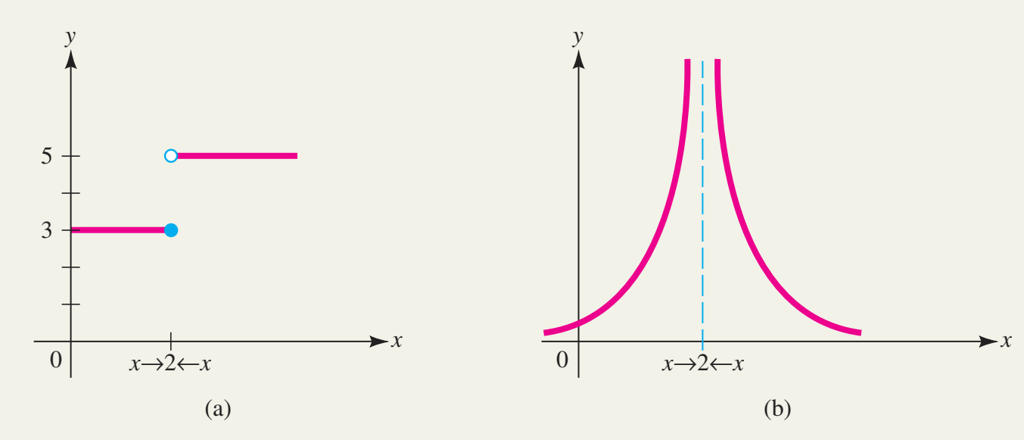
♦ Hình vẽ dưới đây minh họa hai trường hợp không tồn tại lim(x→2)[f(x)〗
2. Các tính chất của giới hạn
Nếu lim┬(𝑥→𝑐)〖𝑓(𝑥)〗 và lim┬(𝑥→𝑐)〖𝑔(𝑥)〗 tồn tại thì:♦ lim┬(𝑥→𝑐)[𝑓(𝑥)+𝑔(𝑥)]=lim┬(𝑥→𝑐)〖𝑓(𝑥) +lim┬(𝑥→𝑐)〖𝑔(𝑥)〗
♦ lim┬(𝑥→𝑐)[𝑓(𝑥)−𝑔(𝑥)]=lim┬(𝑥→𝑐)〖𝑓(𝑥)〗−lim┬(𝑥→𝑐)〖𝑔(𝑥)〗
♦ lim┬(𝑥→𝑐)[𝑘.𝑓(𝑥)]=𝑘.lim┬(𝑥→𝑐)〖𝑓(𝑥)〗 với 𝑘 là hằng số bất kỳ
♦ lim┬(𝑥→𝑐)[𝑓(𝑥).𝑔(𝑥)]=lim┬(𝑥→𝑐)〖𝑓(𝑥)〗.lim┬(𝑥→𝑐)〖𝑔(𝑥)〗
♦ lim┬(𝑥→𝑐)〖𝑓(𝑥)/𝑔(𝑥) 〗=lim┬(𝑥→𝑐)𝑓(𝑥)/lim┬(𝑥→𝑐)〖𝑔(𝑥)〗nếu lim┬(𝑥→𝑐)〖𝑔(𝑥)〗≠0
♦ lim┬(𝑥→𝑐)〖[𝑓(𝑥)]^𝑝 〗=[lim┬(𝑥→𝑐)〖𝑓(𝑥)〗 ]^𝑝 nếu [lim┬(𝑥→𝑐)〖𝑓(𝑥)〗 ]^𝑝tồn tại
Giới hạn của hàm tuyến tính
♦ lim┬(x→c)k=k;
♦ lim┬(x→c)x=c
Giới hạn của đa thức và phân thức
Nếu p(x) và q(x) là các đa thức thì
♦ lim┬(x→c)p(x)=p(c)
♦〖 lim┬(x→c)〗〖p(x)/q(x) 〗=p(c)/q(c) nếu q(c)≠0
Ví dụ 1: Tính giới hạn của đa thức, phân thức:
Tính các giới hạn sau:
a) lim┬(x→-1)(3x^3-4x+8)
b) lim┬(x→1)〖(3x^3-8)/(x-2)〗
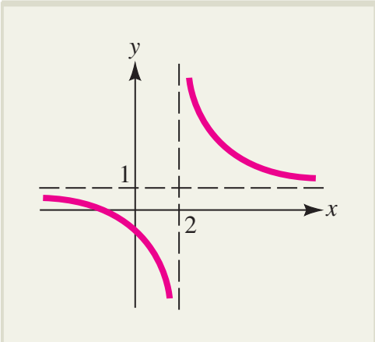
Ví dụ 2: Chứng minh giới hạn không tồn tại:
Tính giới hạn:
lim┬(𝑥→2)〖(𝑥+1)/(𝑥−2)〗
Ví dụ 3: Sử dụng biến đổi đại số để tìm giới hạn
Tính giới hạn:
a) lim┬(𝑥→1)〖(𝑥^2−1)/(𝑥^2−3𝑥+2)〗
b) lim┬(𝑥→1) (√𝑥−1)/(𝑥−1)
Tính các giới hạn sau:
a) lim┬(x→-1)(3x^3-4x+8)
b) lim┬(x→1)〖(3x^3-8)/(x-2)〗
Ví dụ 2: Chứng minh giới hạn không tồn tại:
Tính giới hạn:
lim┬(𝑥→2)〖(𝑥+1)/(𝑥−2)〗

Ví dụ 3: Sử dụng biến đổi đại số để tìm giới hạn
Tính giới hạn:
a) lim┬(𝑥→1)〖(𝑥^2−1)/(𝑥^2−3𝑥+2)〗
b) lim┬(𝑥→1) (√𝑥−1)/(𝑥−1)
3. Các giới hạn liên quan đến vô hạn
Giới hạn tại vô hạn:
♦ Nếu các giá trị của hàm 𝑓(𝑥) tiến gần đến số 𝐿 khi 𝑥 tăng không bị chặn thì ta viết
lim┬(𝑥→+∞)𝑓(𝑥)=𝐿
♦ Nếu các giá trị của hàm 𝑓(𝑥) tiến gần đến số 𝐿 khi 𝑥 giảm không bị chặn thì ta viết
lim┬(𝑥→−∞)𝑓(𝑥)=𝑀
Chú ý:
Nếu 𝐴 và 𝑘 là các hằng số với 𝑘>0 và 𝑥^𝑘 xác định với mọi 𝑥 thì
lim┬(𝑥→+∞)〖𝐴/𝑥^𝑘 〗=0 và lim┬(𝑥→−∞)〖𝐴/𝑥^𝑘 〗=0
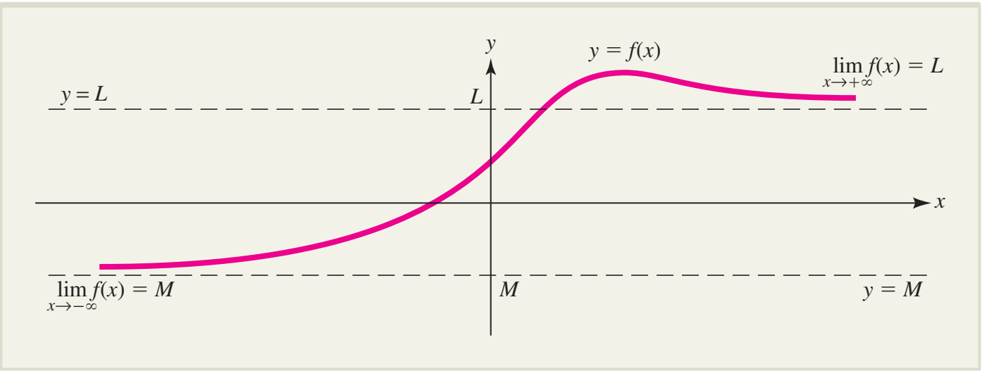
Về mặt hình học:
Các đường thẳng 𝑦=𝐿, 𝑦=𝑀 được gọi là các tiệm cận ngang của đồ thị hàm số 𝑦=𝑓(𝑥)
Ví dụ: Ứng dụng giới hạn tại vô hạn
Nếu hàm lượng Ni-tơ có trong một thửa đất là 𝑁 thì sản lượng 𝑌 của vụ mùa trồng trên thửa đất được tính bởi công thức của Michalelis-Menten:
𝑌(𝑁)=𝐴𝑁/(𝐵+𝑁), 𝑁≥0
Trong đó 𝐴 và 𝐵 là các hằng số dương.
Điều gì sẽ xảy ra với sản lượng của vụ mùa nếu lượng Ni-tơ trong đất tăng không bị chặn?
lim┬(𝑥→+∞)𝑓(𝑥)=𝐿
♦ Nếu các giá trị của hàm 𝑓(𝑥) tiến gần đến số 𝐿 khi 𝑥 giảm không bị chặn thì ta viết
lim┬(𝑥→−∞)𝑓(𝑥)=𝑀
Chú ý:
Nếu 𝐴 và 𝑘 là các hằng số với 𝑘>0 và 𝑥^𝑘 xác định với mọi 𝑥 thì
lim┬(𝑥→+∞)〖𝐴/𝑥^𝑘 〗=0 và lim┬(𝑥→−∞)〖𝐴/𝑥^𝑘 〗=0
Về mặt hình học:
Các đường thẳng 𝑦=𝐿, 𝑦=𝑀 được gọi là các tiệm cận ngang của đồ thị hàm số 𝑦=𝑓(𝑥)

Ví dụ: Ứng dụng giới hạn tại vô hạn
Nếu hàm lượng Ni-tơ có trong một thửa đất là 𝑁 thì sản lượng 𝑌 của vụ mùa trồng trên thửa đất được tính bởi công thức của Michalelis-Menten:
𝑌(𝑁)=𝐴𝑁/(𝐵+𝑁), 𝑁≥0
Trong đó 𝐴 và 𝐵 là các hằng số dương.
Điều gì sẽ xảy ra với sản lượng của vụ mùa nếu lượng Ni-tơ trong đất tăng không bị chặn?
Giới hạn vô hạn:
♦ Hàm 𝑓(𝑥) được gọi là có giới hạn vô hạn nếu 𝑓(𝑥) tăng hoặc giảm không bị chặn khi 𝑥→𝑐.
♦ Ký hiệu:
lim┬(𝑥→𝑐)𝑓(𝑥)=+∞ nếu 𝑓(𝑥) tăng không bị chặn khi 𝑥→𝑐
lim┬(𝑥→𝑐)𝑓(𝑥)=−∞ nếu 𝑓(𝑥) giảm không bị chặn khi 𝑥→𝑐
Ví dụ: sử dụng giới hạn vô hạn nghiên cứu lợi nhuận bình quân.
Một nhà sản xuất xác định được rằng khi sản xuất và bán được x trăm đơn vị một loại sản phẩm thì lợi nhuận là P(x)=4x-√x nghìn đô la. Lợi nhuận bình quân sẽ bằng bao nhiêu khi mức sản xuất là rất nhỏ?
♦ Ký hiệu:
lim┬(𝑥→𝑐)𝑓(𝑥)=+∞ nếu 𝑓(𝑥) tăng không bị chặn khi 𝑥→𝑐
lim┬(𝑥→𝑐)𝑓(𝑥)=−∞ nếu 𝑓(𝑥) giảm không bị chặn khi 𝑥→𝑐
Ví dụ: sử dụng giới hạn vô hạn nghiên cứu lợi nhuận bình quân.
Một nhà sản xuất xác định được rằng khi sản xuất và bán được x trăm đơn vị một loại sản phẩm thì lợi nhuận là P(x)=4x-√x nghìn đô la. Lợi nhuận bình quân sẽ bằng bao nhiêu khi mức sản xuất là rất nhỏ?
BÀI TẬP VẬN DỤNG
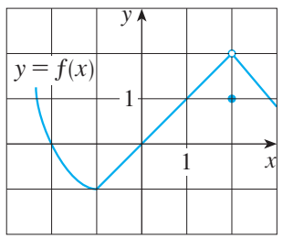
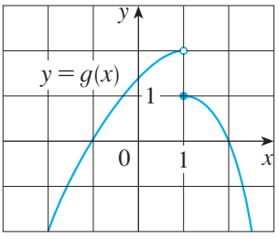
Cho các hàm số 𝑓 và 𝑔 có đồ thị như hình vẽ.
Hãy tính:
a) lim┬(𝑥→2)〖[𝑓(𝑥)+𝑔(𝑥)]〗
b) lim┬(𝑥→1)〖[𝑓(𝑥)+𝑔(𝑥)]〗
c) lim┬(𝑥→0)〖[𝑓(𝑥).𝑔(𝑥)]〗
d) lim┬(𝑥→0)〖𝑓(𝑥)/𝑔(𝑥) 〗
Hãy tính:
a) lim┬(𝑥→2)〖[𝑓(𝑥)+𝑔(𝑥)]〗
b) lim┬(𝑥→1)〖[𝑓(𝑥)+𝑔(𝑥)]〗
c) lim┬(𝑥→0)〖[𝑓(𝑥).𝑔(𝑥)]〗
d) lim┬(𝑥→0)〖𝑓(𝑥)/𝑔(𝑥) 〗


Trên đây là toàn bộ kiến thức về phần "Giới hạn của hàm số" thuộc môn toán cho các nhà kinh tế trường NEU. Hi vọng các bạn sinh viên NEU đã có một bài học bổ ích, đừng quên, Ôn thi sinh viên thường chia sẻ đề thi và tài liệu của các trường đại học toàn quốc ở fanpage: Onthisinhvien.com. Mời bạn ghé qua !
Chúc bạn học tập hiệu quả - đạt kết quả cao!
Xem thêm:
Đạo hàm của tích, của thương và đạo hàm cấp cao
Kỹ thuật tính đạo hàm nhanh chóng
Đào hàm của hàm hợp
Hàm đa biến trong Giải tích

Liên hệ tương tác trực tiếp qua zalo: 0359.286.819 (chị Linh - giải quyết khó khăn môn Nguyên lý kế toán, Kế toán tài chính TẤT CẢ CÁC TRƯỜNG ĐẠI HỌC)
💥Giải đáp FREE các câu hỏi về NGUYÊN LÝ KẾ TOÁN
💥Nhận gia sư 1-1 cấp tốc cho người mất gốc (online/offline)
💥Nhận booking giải bài tập về nhà, đề cương ôn tập , làm mẫu các đề thi (có đáp án và giải thích chi tiết)
Đọc chi tiết dịch vụ tại đây
📍 KHÔNG NHẬN THI HỘ - HỌC LÀ HIỂU BẢN CHẤT