Hàm đa biến | Toán cho các nhà kinh tế
Ngày: 17/12/2023
HÀM ĐA BIẾN
Hàm đa biến là một phần kiến thức quan trọng và xuất hiện trong đề thi nhiều nhất thuộc môn Toán cho các nhà kinh tế. Hàm số được áp dụng vào bài toán kinh tế thực tế, do đó sinh viên cần nắm vững phần kiến thức này để làm tốt những bài tập liên quan phục vụ thi giữa và cuối kì.
Nếu bạn còn băn khoăn về đề thi, vậy hãy click : VÀO ĐÂY, chúng mình có đầy đủ lý thuyết từng chương học môn Toán cho nhà kinh tế và đề thi của trường NEU qua các kì.
I. Định nghĩa
Định nghĩa:
Một hàm n biến là một quy tắc đặt tương ứng mỗi bộ n số thực (x1, x2, ...xn) với một số thực duy nhất, ký hiệu là u = f(x1, x2, ...xn). Hay nói cách khác, ánh xạ
f : D ⊂ Rn → R
(x1, x2, ...xn) → u = f(x1, x2, ...xn)
được gọi là hàm n biến xác định trên D.
Tập hợp D gọi là miền xác định của hàm số f, nghĩa là tập hợp các điểm (x1, x2, ...xn) có nghĩa. Miền xác định của f là tập hợp các giá trị mà f nhận được.
Trường hợp n = 2, ta có hàm hai biến, thường ký hiệu là z = f(x,y)
Trường hợp n = 3 ta có hàm 3 biến thường kí hiệu là u = f(x,y,z)
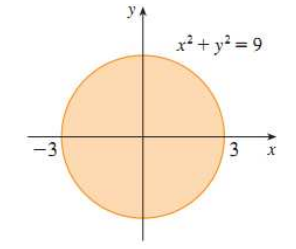
D là tập hợp những điểm nằm trong hay nằm trên đường tròn tâm (0,0) bán kính 3
Ví dụ 1:
Tìm miền xác định của các hàm số sau:
a. f(x,y) = x2 - y + sin(x,y)
b. f(x,y) = √9 - x2 - y2
Một hàm n biến là một quy tắc đặt tương ứng mỗi bộ n số thực (x1, x2, ...xn) với một số thực duy nhất, ký hiệu là u = f(x1, x2, ...xn). Hay nói cách khác, ánh xạ
f : D ⊂ Rn → R
(x1, x2, ...xn) → u = f(x1, x2, ...xn)
được gọi là hàm n biến xác định trên D.
Tập hợp D gọi là miền xác định của hàm số f, nghĩa là tập hợp các điểm (x1, x2, ...xn) có nghĩa. Miền xác định của f là tập hợp các giá trị mà f nhận được.
Trường hợp n = 2, ta có hàm hai biến, thường ký hiệu là z = f(x,y)
Trường hợp n = 3 ta có hàm 3 biến thường kí hiệu là u = f(x,y,z)
D là tập hợp những điểm nằm trong hay nằm trên đường tròn tâm (0,0) bán kính 3
Ví dụ 1:
Tìm miền xác định của các hàm số sau:
a. f(x,y) = x2 - y + sin(x,y)
b. f(x,y) = √9 - x2 - y2
Giải
a. Miền xác định: D = R2
b. f xác định ⇔ 9 - x2 - y2 >= 0 ⇔ x2 + y2 =< 9
Miền xác định D = {(x, y) ∈ R2 | x2 + y2 =< 9 }
b. f xác định ⇔ 9 - x2 - y2 >= 0 ⇔ x2 + y2 =< 9
Miền xác định D = {(x, y) ∈ R2 | x2 + y2 =< 9 }
II. Đồ thị hàm hai biến
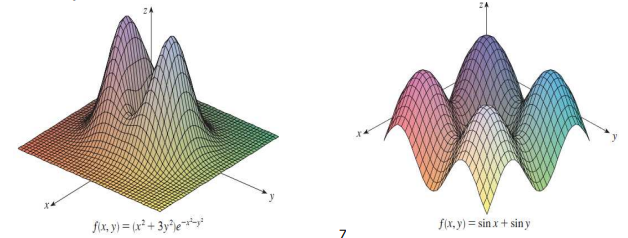
Đồ thị của hàm số 2 biến f(x,y) xác định trên D là tập hợp tất cả các điểm (x,y,z) ∈ R3 sao cho z = f(x,y) và (x,y) ∈ D
Ví dụ: Đồ thị của một số hàm hai biến
III. Một số hàm hai biến số trong kinh tế:
1. Hàm sản xuất:
Là hàm mô tả mối quan hệ phụ thuộc của sản lượng vào vốn lao động
Q = f(K,L)
Trong đó
K: vốn
L: lao động
K: vốn
L: lao động
2. Hàm tổng chi phí:
C = wk.K + wl.L + C0
Trong đó:
wk: giá thuê một đơn vị vốn
wl: giá thuê một đơn vị lao động
C0: chi phí cố định
wk: giá thuê một đơn vị vốn
wl: giá thuê một đơn vị lao động
C0: chi phí cố định
3. Hàm tổng doanh thu
R = P.Q = P.f(K.L)
Trong đó
P là giá thị trường của một đơn vị lao động
Vậy là OTSV đã giới thiệu đến bạn đầy đủ kiến thức về Hàm đa biến thuộc môn Toán kinh tế. Hãy ôn tập thật kì phần này vì bạn sẽ còn gặp lại nó nhiều trong các chương sau. Nếu cảm thấy quá khó khăn thì đừng quên chúng mình có Khóa học đầy đủ Toán cho các nhà kinh tế có thể trả lời tất cả các câu hỏi của bạn liên quan đến môn học.
Chúc bạn ôn tập hiệu quả !
Tham khảo thêm:
Phép thế trong Toán cao cấp 1
Quy luật cơ bản trong kinh tế
Trắc nghiệm môn Quản trị kinh doanh
P là giá thị trường của một đơn vị lao động
Vậy là OTSV đã giới thiệu đến bạn đầy đủ kiến thức về Hàm đa biến thuộc môn Toán kinh tế. Hãy ôn tập thật kì phần này vì bạn sẽ còn gặp lại nó nhiều trong các chương sau. Nếu cảm thấy quá khó khăn thì đừng quên chúng mình có Khóa học đầy đủ Toán cho các nhà kinh tế có thể trả lời tất cả các câu hỏi của bạn liên quan đến môn học.
Chúc bạn ôn tập hiệu quả !
Tham khảo thêm:
Phép thế trong Toán cao cấp 1
Quy luật cơ bản trong kinh tế
Trắc nghiệm môn Quản trị kinh doanh