Phép thế trong toán cao cấp và bào tập vận dụng có giải chi tiết
Ngày: 17/12/2023
PHÉP THẾ TRONG TOÁN CAO CẤP
Phép thế là phần kiến thức quan trọng đầu tiên của môn học toán cao cấp, nếu không nắm chắc phần này bạn sẽ rất khó khăn để học các phần sau. Chính vì vậy, hãy xem xét thật kĩ bài viết dưới đây để hiểu rõ bản chất về Phép thế trong toán cao cập và kết hợp làm bài tập vận dụng nhé !
Luyện đề trắc nghiệm Toán cao cấp: TẠI ĐÂY => Học đầy đủ: Ở ĐÂY
Luyện đề trắc nghiệm Toán cao cấp: TẠI ĐÂY => Học đầy đủ: Ở ĐÂY
PHÉP THẾ
1.1 Định nghĩa phép thế
a. Giả sử tập hợp Xn = { 1, 2, 3,..., n}, {n >= 1}. Một song ánh 𝛔: Xn => Xn được gọi là một phép thế trên tập hợp Xn
Nói riêng, song ảnh đồng nhất được gọi là phép thế đồng nhất
b. Một phép thế 𝝉 trên tập hợp Xn được gọi là một chuyển trí hai phần tử i, j thuộc Xn nếu 𝝉(i) = j, 𝝉(j) = i và 𝝉(k) = k, với mọi k ∈ Xn, k ≠ i, k ≠ j. Nó còn được kí hiệu bởi (i, j)
Nói một cách đơn giản hơn thì chuyển trí chỉ hoán vị hai phân tử nào đó của Xn, còn giữ nguyên mọi phần tử khác.
Tập hợp tất cả các phép thế trên tập hợp Xn được kí hiệu bởi Sn.
Phép thế 𝛔: Xn → Xn được biểu diễn như sau:
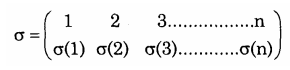
trong đó 𝛔(i) là ảnh của phần tử i ∈ Xn được viết ở dòng dưới, trong cùng một cột với i.
Chú ý: ảnh của các phần tử của tập Xn qua mỗi phép thế cho ta một hoán vị trên tập Xn. Ngược lại, mỗi hoán vị lại xác định một phép thế, chẳng hạn hoán vị (3, 4, 1, 2) xác định phép thế như sau:
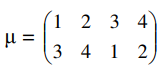
trên tập hợp X4. Vì thế số các phép trên tập Xn bằng số các hoán vị trên tập ấy; nghĩa là bằng n!. Như vậy, tập Sn có n! phần tử.
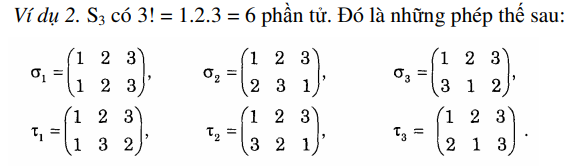
Nói riêng, song ảnh đồng nhất được gọi là phép thế đồng nhất
b. Một phép thế 𝝉 trên tập hợp Xn được gọi là một chuyển trí hai phần tử i, j thuộc Xn nếu 𝝉(i) = j, 𝝉(j) = i và 𝝉(k) = k, với mọi k ∈ Xn, k ≠ i, k ≠ j. Nó còn được kí hiệu bởi (i, j)
Nói một cách đơn giản hơn thì chuyển trí chỉ hoán vị hai phân tử nào đó của Xn, còn giữ nguyên mọi phần tử khác.
Tập hợp tất cả các phép thế trên tập hợp Xn được kí hiệu bởi Sn.
Phép thế 𝛔: Xn → Xn được biểu diễn như sau:
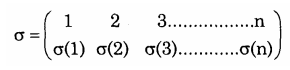
trong đó 𝛔(i) là ảnh của phần tử i ∈ Xn được viết ở dòng dưới, trong cùng một cột với i.
Chú ý: ảnh của các phần tử của tập Xn qua mỗi phép thế cho ta một hoán vị trên tập Xn. Ngược lại, mỗi hoán vị lại xác định một phép thế, chẳng hạn hoán vị (3, 4, 1, 2) xác định phép thế như sau:
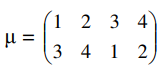
trên tập hợp X4. Vì thế số các phép trên tập Xn bằng số các hoán vị trên tập ấy; nghĩa là bằng n!. Như vậy, tập Sn có n! phần tử.
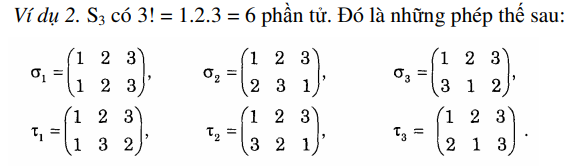
1.2 Nghịch thế
Định nghĩa: Giả sử mà một phép thế trên tập Xn với i, j ∈ Xn, i ≠ j, ta nói cặp 𝛔(i), 𝛔(j) là một nghịch thế của 𝛔 nếu i < j nhưng 𝛔(i) > 𝛔(j)
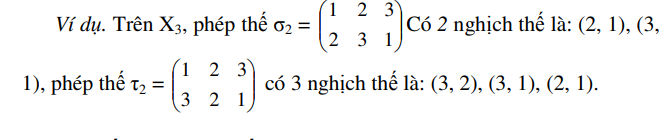
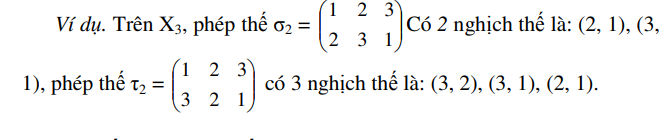
1.3 Dấu của phép thế
Định nghĩa: Ta gọi phép thế là 𝛔 là một phép thế chẵn nên nó có một số chẵn nghịch thế. 𝛔 được gọi là phép thế lẻ nếu nó có một số lẻ nghịch thế.
Ta gán cho mỗi phép thế chẵn một giá trị bằng +1, mỗi phép thế lẻ một giá trị bằng -1.
Giá trị này của phép thế 𝛔 được gọi là dấu của 𝛔 và được kí hiệu bởi sgn(𝛔)
Như vậy, theo định nghĩa thì:
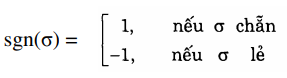
Ta gán cho mỗi phép thế chẵn một giá trị bằng +1, mỗi phép thế lẻ một giá trị bằng -1.
Giá trị này của phép thế 𝛔 được gọi là dấu của 𝛔 và được kí hiệu bởi sgn(𝛔)
Như vậy, theo định nghĩa thì:
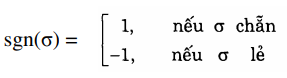
Hệ quả 1:
trong đó {i, j} chạy khắp các tập con gồm 2 phần tử của Xn. Rõ ràng số nhân tử ở tử số và mẫu bằng nhau. Ta sẽ chứng minh: nếu tử số có nhân tử i - j thì mẫu số có i - j hoặc j - i. Vì 𝛔 là một song ánh nên ứng với nhân tử i - j tồn tại h, k ∈ Xn sao cho 𝛔(h) = i, 𝛔(k) = j. Nếu tử số có h - k thì mẫu số có 𝛔(h) - 𝛔(k) hay i - j , nếu tử số có k - h thì mẫu số có j = i.
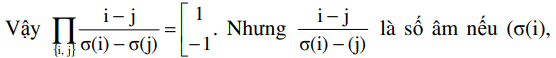
𝛔(i) là một nghịch thế và là một số dương nếu trái lại. Từ đó suy ra điều phải chứng minh
Hệ quả 2
Với 2 phép thêm 𝛔 và 𝞵 trên Xn ta có:
Hệ quả 3
Mọi chuyển trí đều là phép thế lẻ:
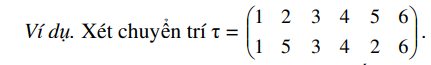
Các nghịch thế đứng ở dòng thứ hai, tức là dòng chứa các 𝝉(i). Số 1 bé hơn và số 6 lớn hơn mọi số trong dòng nên chúng không tham gia vào nghịch thế. Do đó chỉ có:
- Các nghịch thế dạng (5, r): (5, 3), (5, 4), (5, 2)
- Các nghịch thế dạng (s, 2): (3, 2), (4, 2), (5, 2)
Vì nghịch thế (5, 2) đã được kể 2 lần nên chỉ có 5 nghịch thế. Vậy 𝝉 là phép thể lẻ
Nếu bạn đọc muốn chứng minh hệ quả này có thể dựa trên các lí giải ở ví dụ vừa nêu.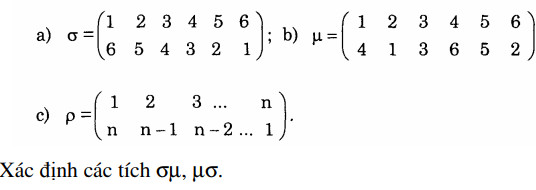
Giải
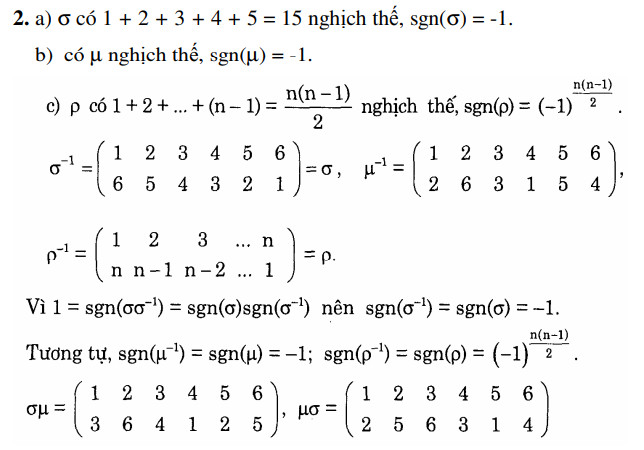
Trên đây là toàn bộ kiến thức về Phép thế trong môn Toán cao cấp kèm theo bài tập vận dụng để các bạn dễ dàng luyện tập. Hi vọng OTSV đã hỗ trợ được bạn trong quá trình học tập phần kiến thức này, và đừng quên để lại phản hồi tích cực dưới bài viết để chúng mình có động lực thực hiện thêm nhiều bài viết hay nhé !!!
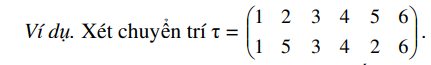
Các nghịch thế đứng ở dòng thứ hai, tức là dòng chứa các 𝝉(i). Số 1 bé hơn và số 6 lớn hơn mọi số trong dòng nên chúng không tham gia vào nghịch thế. Do đó chỉ có:
- Các nghịch thế dạng (5, r): (5, 3), (5, 4), (5, 2)
- Các nghịch thế dạng (s, 2): (3, 2), (4, 2), (5, 2)
Vì nghịch thế (5, 2) đã được kể 2 lần nên chỉ có 5 nghịch thế. Vậy 𝝉 là phép thể lẻ
Nếu bạn đọc muốn chứng minh hệ quả này có thể dựa trên các lí giải ở ví dụ vừa nêu.
Bài tập phép thế
Bài 1: Thực hiện các phép nhân sau đây, viết các phép thế thu được thành tích các xích rời nhau và tính dấu của chúng. Xác định thêm ánh xạ ngược của các phép thế thu được.
Giải:
Bài 2: Cho phép thế σ ∈ Sn. Đặt τ(i) = σ(n+1−i) với 1≤i≤n.Khi đó τ cũng là một phép thế cấp n.Giả sử số nghịch thế của σ là k thì số nghịch thế của τbằng bao nhiêu?
Giải
Bài 3: Với mỗi phép thế sau hãy xác định dấu của nó, tìm phép thế nghịch đảo và dấu của phép thế nghịch đảo:
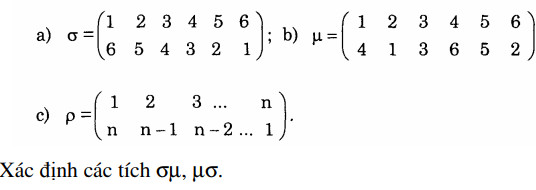
Giải
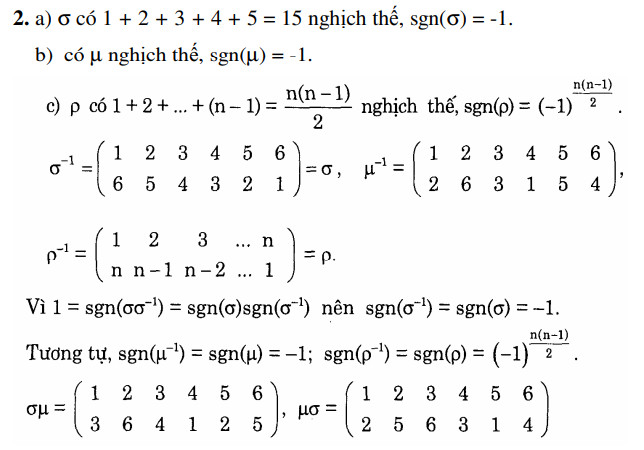
Trên đây là toàn bộ kiến thức về Phép thế trong môn Toán cao cấp kèm theo bài tập vận dụng để các bạn dễ dàng luyện tập. Hi vọng OTSV đã hỗ trợ được bạn trong quá trình học tập phần kiến thức này, và đừng quên để lại phản hồi tích cực dưới bài viết để chúng mình có động lực thực hiện thêm nhiều bài viết hay nhé !!!