Tích phân bất định và phương trình vi phân - phép toán tích phân - Toán cho các nhà kinh tế neu
Ngày: 27/12/2023
TOÁN CHO CÁC NHÀ KINH TẾ NEU
PHÉP TOÁN TÍCH PHÂN
Bài 1: Tích phân bất định và phương trình vi phân
Trong bài 1 của chương học "Phép toán tích phân" chúng ta cùng nhau tìm hiểu và tính tích phân bất định, phương trình vi phân, bài toán giá trị ban đầu và thiết lập, giải phương trình vi phân biến số. Bài viết là tổng hợp những kiến thức trọng tâm sẽ xuất hiện trong đề thi môn học này tại NEU, do vậy các bạn sinh viên hãy đọc thật kĩ nhé !


1. Khái niệm nguyên hàm
Định nghĩa
Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) nếu
𝐹^′ (𝑥)=𝑓(𝑥) ∀𝑥∈𝐷
hay:
𝑑𝐹/𝑑𝑥=𝑓(𝑥) ∀𝑥∈𝐷
Minh họa:
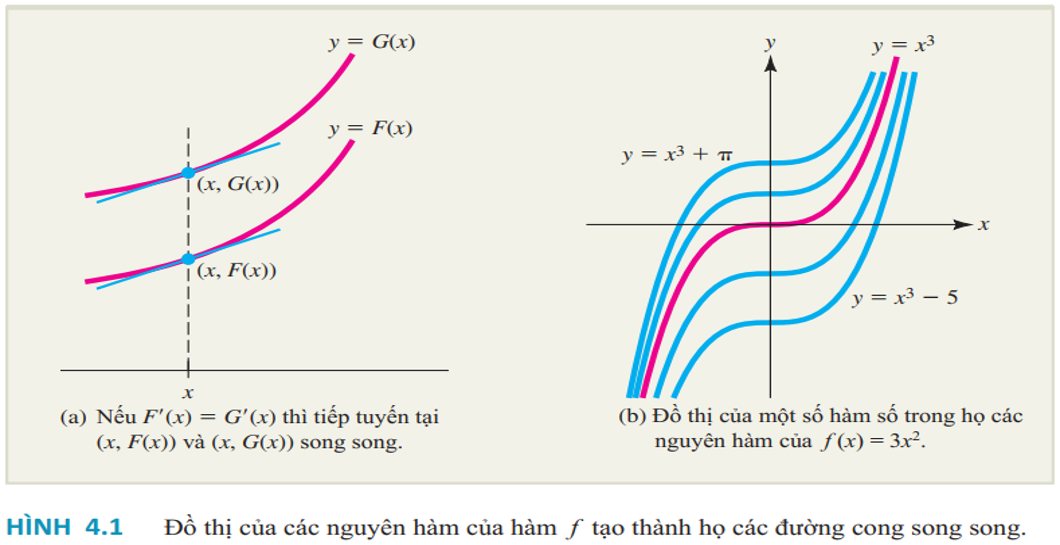
Ví dụ 1: Kiểm tra một nguyên hàm
1. Chứng tỏ rằng hàm số
F(𝑥)=𝑥^3/3+𝑥^2/2+𝑥+2020
là một nguyên hàm của hàm số
𝑓(𝑥)=𝑥^2+𝑥+1
2. Chứng tỏ rằng nếu 𝐹(𝑥) là một nguyên hàm của 𝑓(𝑥) thì F(𝑥)+𝐶 cũng là một nguyên hàm của 𝑓(𝑥) (Với C là một hằng số nào đó)

Ví dụ 1: Kiểm tra một nguyên hàm
1. Chứng tỏ rằng hàm số
F(𝑥)=𝑥^3/3+𝑥^2/2+𝑥+2020
là một nguyên hàm của hàm số
𝑓(𝑥)=𝑥^2+𝑥+1
2. Chứng tỏ rằng nếu 𝐹(𝑥) là một nguyên hàm của 𝑓(𝑥) thì F(𝑥)+𝐶 cũng là một nguyên hàm của 𝑓(𝑥) (Với C là một hằng số nào đó)
Xem thêm: Giới hạn của hàm số
Tính chất cơ bản của nguyên hàm
Nếu F (x) là một nguyên hàm của hàm số liên tục f (x) thì mọi nguyên hàm của hàm số f (x) đều có dạng:
G(x) = F(x) + C với C là hằng số nào đó
2. Khái niệm tích phân bất định
Họ tất cả các nguyên hàm của f (x) được ký hiệu là
∫𝑓 (𝑥) 𝑑𝑥 = 𝐹(𝑥) + 𝐶
và được gọi là tích phân bất định của f (x).
Ở đó F(x) là một nguyên hàm của hàm số f (x).
Chẳng hạn,
Ở đó F(x) là một nguyên hàm của hàm số f (x).
Chẳng hạn,
∫sin𝑥 𝑑𝑥 = −cos𝑥+ 𝐶
Vì 𝐹(𝑥)=−cos𝑥 là một nguyên hàm của f(𝑥)=sin𝑥.
Minh họa:
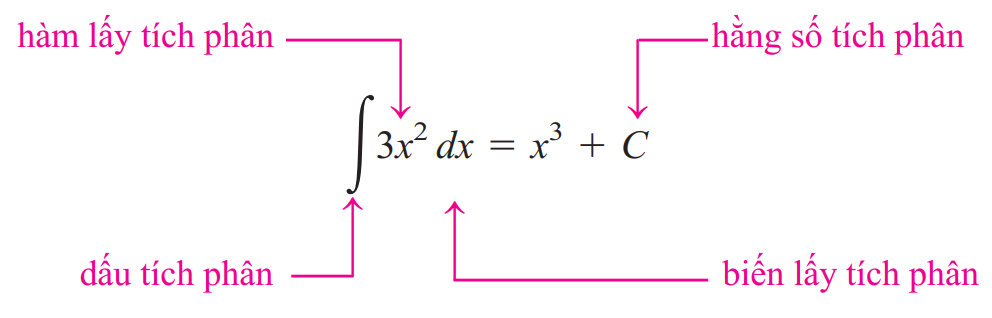
Minh họa:
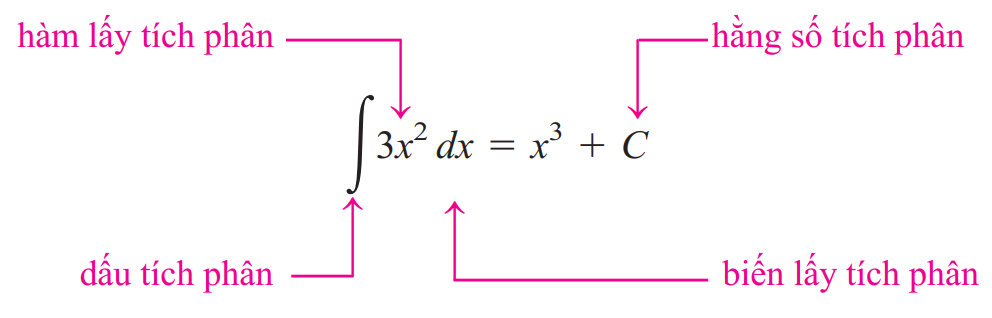
Một số quy tắc tích phân


Ví dụ 2: Tính một số tích phân bất định cơ bản
Hãy tính các tích phân sau:
a. ∫5𝑑𝑥 b. ∫𝑥15 𝑑𝑥
c. ∫2/(3𝑥√𝑥) 𝑑𝑥 d. ∫𝑒−5𝑥 𝑑𝑥
Ví dụ 3: Tìm hàm số từ hàm tốc độ
Tìm hàm số 𝑓(𝑥) biết độ dốc của tiếp tuyến là 3𝑥^2+1 với mọi giá trị của x và đồ thị của 𝑓(𝑥) đi qua điểm (2, 6).
Ví dụ 4: Tìm tổng chi phí từ chi phí cận biên
Chi phí cận biên của một loại sản phẩm của một nhà sản xuất là
3𝑞2 −60𝑞 + 400
đô-la mỗi đơn vị khi 𝑞 đơn vị được sản xuất. Chi phí để sản xuất 2 đơn vị đầu tiên là 900 đô-la. Hãy tính chi phí để sản xuất 5 đơn vị đầu tiên?
3. Phương trình vi phân
Một loại phương trình vi phân tổng quát hơn, được gọi là phương trình phân ly biến số, có dạng:
𝑑𝑦/𝑑𝑥=ℎ(𝑥)/𝑔(𝑦)
và có thể giải được bằng cách biến đổi đại số đưa phương trình về tách biến (mỗi vế của nó chỉ chứa một biến), cụ thể là:
𝑔(𝑦)𝑑𝑦 = ℎ(𝑥)𝑑𝑥
Sau đó lấy tích phân hai vế, ta được:
∫𝑔(𝑦)𝑑𝑦=∫ℎ(𝑥)𝑑𝑥
Ví dụ 1: Giải phương trình vi phân phân ly biến số
Tìm nghiệm tổng quát của phương trình vi phân
𝑑𝑦/𝑑𝑥=2𝑥/𝑦2
Ví dụ 2: Giải phương trình vi phân để tìm doanh thu
Willis Jenkins sở hữu một giếng dầu dự kiến sẽ khai thác được 200 thùng dầu thô mỗi tháng, và với tốc độ đó, giếng dầu sẽ cạn trong 3 năm. Người ta ước tính rằng t tháng kể từ bây giờ, giá dầu thô sẽ là
𝑝(𝑡)=140+24√𝑡
đô-la mỗi thùng. Nếu Willis có
thể bán dầu ngay khi được khai thác khỏi mặt đất thì tổng doanh thu dự kiến anh ta nhận được trong thời gian hoạt động của giếng dầu là bao nhiêu?
Sử dụng phương trình vi phân để tính lãi gộp liên tục
Một tài khoản tiết kiệm có giá trị B(t) tại thời điểm t được gọi là có lãi gộp liên tục nếu tốc độ tăng trưởng phần trăm của tài khoản bằng lãi suất hiện hành. Chẳng hạn, nếu lãi suất là 5%, ta có:

Thông thường, lãi suất được biểu diễn ở dạng thập phân, vì vậy ta viết 5% thành r 0.05 và công thức gộp liên tục có thể biểu diễn theo tốc độ tăng trưởng tương đối của B(t):

Nếu P đô-la (tiền gốc) được đầu tư vào một tài khoản trả lãi theo phương thức gộp liên tục với lãi suất hàng năm là r thì tài khoản có giá trị:

Thông thường, lãi suất được biểu diễn ở dạng thập phân, vì vậy ta viết 5% thành r 0.05 và công thức gộp liên tục có thể biểu diễn theo tốc độ tăng trưởng tương đối của B(t):

Nếu P đô-la (tiền gốc) được đầu tư vào một tài khoản trả lãi theo phương thức gộp liên tục với lãi suất hàng năm là r thì tài khoản có giá trị:
𝑩(𝒕)=𝑷𝒆𝒓𝒕 đô-la sau t năm.
Tìm công thức tính lãi gộp liên tục
Giải bài toán giá trị ban đầu để chứng tỏ rằng nếu P đô-la được đầu tư với tỷ lệ lãi suất được tính gộp liên tục hàng năm là r (r được viết dưới dạng số thập phân) thì giá trị (tương lai) của khoản đầu tư này sau t năm là: 𝑩(𝒕)=𝑷𝒆𝒓𝒕 đô-la
CÁC DẠNG BÀI TẬP LIÊN QUAN
1. Hãy tính các tích phân sau
a) ∫(𝑒^𝑥/2+𝑥√𝑥) 𝑑𝑥
b) ∫(√(𝑥^3 )−1/(2√𝑥)+√2) 𝑑𝑥
c) ∫((𝑥^2+3𝑥−2)/√𝑥) 𝑑𝑥
d) ∫〖𝑦^3 (2𝑦+1/𝑦) 〗 𝑑𝑦
e) ∫〖𝑒^(−0,02𝑡) (𝑒^(−0,13𝑡)+4) 〗 𝑑𝑡
2. Giải bài toán giá trị ban đầu với 𝑦=𝑓(𝑥)
𝑑𝑦/𝑑𝑥=3𝑥−2
với 𝑦=2 khi 𝑥=−1.
𝑑𝑦/𝑑𝑥=(𝑥+1)/√𝑥
với 𝑦=5 khi" " 𝑥=4.
3. Giải phương trình phân ly biến số với giá trị ban đầu tương ứng
𝑑𝑦/𝑑𝑥=𝑒^(𝑥+𝑦)
với 𝑦=0 khi 𝑥=0
b) 𝑑𝑦/𝑑𝑥=√(𝑦/𝑥)
với 𝑦=1 khi" " 𝑥=1.
4. Một nhà sản xuất ước tính chi phí cận biên từ việc sản xuất q đơn vị một loại hàng hóa là:
𝐶^′ (𝑞)=3𝑞^2−24𝑞+48
đô-la mỗi đơn vị. Nếu chi phí sản xuất 10 đơn vị là 5,000 đô-la thì chi phí để sản xuất 30 đơn vị là bao nhiêu?
5. Lợi nhuận cận biên của một loại hàng hóa là 𝑃(𝑞)=100−2𝑞 khi q đơn vị được sản xuất. Khi 10 đơn vị hàng hóa được sản xuất thì lợi nhuận là 700 đô-la.
Tìm hàm lợi nhuận P(q).
Xác định mức sản lượng q để lợi nhuận đạt giá trị lớn nhất? Lợi nhuận lớn nhất là bao nhiêu?
a) ∫(𝑒^𝑥/2+𝑥√𝑥) 𝑑𝑥
b) ∫(√(𝑥^3 )−1/(2√𝑥)+√2) 𝑑𝑥
c) ∫((𝑥^2+3𝑥−2)/√𝑥) 𝑑𝑥
d) ∫〖𝑦^3 (2𝑦+1/𝑦) 〗 𝑑𝑦
e) ∫〖𝑒^(−0,02𝑡) (𝑒^(−0,13𝑡)+4) 〗 𝑑𝑡
2. Giải bài toán giá trị ban đầu với 𝑦=𝑓(𝑥)
𝑑𝑦/𝑑𝑥=3𝑥−2
với 𝑦=2 khi 𝑥=−1.
𝑑𝑦/𝑑𝑥=(𝑥+1)/√𝑥
với 𝑦=5 khi" " 𝑥=4.
3. Giải phương trình phân ly biến số với giá trị ban đầu tương ứng
𝑑𝑦/𝑑𝑥=𝑒^(𝑥+𝑦)
với 𝑦=0 khi 𝑥=0
b) 𝑑𝑦/𝑑𝑥=√(𝑦/𝑥)
với 𝑦=1 khi" " 𝑥=1.
4. Một nhà sản xuất ước tính chi phí cận biên từ việc sản xuất q đơn vị một loại hàng hóa là:
𝐶^′ (𝑞)=3𝑞^2−24𝑞+48
đô-la mỗi đơn vị. Nếu chi phí sản xuất 10 đơn vị là 5,000 đô-la thì chi phí để sản xuất 30 đơn vị là bao nhiêu?
5. Lợi nhuận cận biên của một loại hàng hóa là 𝑃(𝑞)=100−2𝑞 khi q đơn vị được sản xuất. Khi 10 đơn vị hàng hóa được sản xuất thì lợi nhuận là 700 đô-la.
Tìm hàm lợi nhuận P(q).
Xác định mức sản lượng q để lợi nhuận đạt giá trị lớn nhất? Lợi nhuận lớn nhất là bao nhiêu?
Trên đây là toàn bộ kiến thức về phần "Tích phân bất định và phương trình vi phân" của phần phép toán tích phân thuộc môn toán cho các nhà kinh tế trường NEU. Hi vọng các bạn sinh viên NEU đã có một bài học bổ ích, đừng quên, Ôn thi sinh viên thường chia sẻ đề thi và tài liệu của các trường đại học toàn quốc ở fanpage: Onthisinhvien.com. Mời bạn ghé qua !
Xem thêm:
Giới hạn của hàm số
Đạo hàm của tích, của thương và đạo hàm cấp cao
Kỹ thuật tính đạo hàm nhanh chóng
Đào hàm của hàm hợp
Hàm đa biến trong Giải tích

Liên hệ tương tác trực tiếp qua zalo: 0359.286.819 (chị Linh - giải quyết khó khăn môn Nguyên lý kế toán, Kế toán tài chính TẤT CẢ CÁC TRƯỜNG ĐẠI HỌC)
💥Giải đáp FREE các câu hỏi về NGUYÊN LÝ KẾ TOÁN
💥Nhận gia sư 1-1 cấp tốc cho người mất gốc (online/offline)
💥Nhận booking giải bài tập về nhà, đề cương ôn tập , làm mẫu các đề thi (có đáp án và giải thích chi tiết)
Đọc chi tiết dịch vụ tại đây
📍 KHÔNG NHẬN THI HỘ - HỌC LÀ HIỂU BẢN CHẤT