BÀI TẬP KINH TẾ LƯỢNG CHƯƠNG 1: MÔ HÌNH HỒI QUY TUYẾN TÍNH HAI BIẾN có đáp án
Ngày: 19/12/2023
KINH TẾ LƯỢNG
BÀI TẬP CHƯƠNG 1: MÔ HÌNH HỒI QUY TUYẾN TÍNH HAI BIẾN
Kinh tế lượng là môn học đòi hỏi các bạn phải luyện tập liên tục nếu không khi nhìn vào đề thi bạn sẽ thấy mọi thứ đều thật lạ lẫm. Môn học này, bắt đầu từ chương 1 đã có nhiều kiến thức 'bổ vào đầu' sinh viên, do đó bạn nên xem kỹ bài viết này để có tài liệu làm bài tập sớm nhất.
Ôn thi trắc nghiệm KINH TẾ LƯỢNG UEH
Ôn thi trắc nghiệm KINH TẾ LƯỢNG NEU ⇒ Học đầy đủ full chương trình TẠI ĐÂY
Bài tập 1.1
Trong các mô hình sau, mô hình nào là mô hình hồi quy tuyến tính
a. Y = β1 + β2X2 + u
b. Y = β1 + β2.Ln(X) + u
c. Y = β1 + β2.1/X + u
d. Ln(Y) = β1 + β2X + u
e. Ln(Y) = β1 + β2.Ln(X) + u
f. Y = 1/(β1 + β2X) + u
a. Y = β1 + β2X2 + u
b. Y = β1 + β2.Ln(X) + u
c. Y = β1 + β2.1/X + u
d. Ln(Y) = β1 + β2X + u
e. Ln(Y) = β1 + β2.Ln(X) + u
f. Y = 1/(β1 + β2X) + u
Bài tập 1.2
Giải thích ý nghĩa của hệ số góc (và hệ số chặn nếu có thể) trong các mô hình hồi quy tổng thể sau. Các hệ số mang dấu như thế nào thì phù hợp với lý thuyết kinh tế?
(a) CT = β1 + β2.TN + u với CT là chi tiêu, TN là thu nhập của hộ gia đình
(b) Q = β1 + β2.P + u với Q là lượng bán, P là giá bán của một loại hàng hóa bình thường
(c) TC = β1 + β2.Q+ u với TC là tổng chi phí, Q là sản lượng của doanh nghiệp
(d) EX = β1 + β2.GDP + u với EX là xuất khẩu, GDP là tổng sản phẩm quốc nội
(e) GDP = β1 + β2.FDI + u với FDI là đầu tư trực tiếp nước ngoài
(f) EX = β1 + β2.USD + u với USD là giá đồng đôla (VND / 1USD)
(g) M = β1 + β2.R + u với M là cầu về tiền mặt, R là lãi suất
(a) CT = β1 + β2.TN + u với CT là chi tiêu, TN là thu nhập của hộ gia đình
(b) Q = β1 + β2.P + u với Q là lượng bán, P là giá bán của một loại hàng hóa bình thường
(c) TC = β1 + β2.Q+ u với TC là tổng chi phí, Q là sản lượng của doanh nghiệp
(d) EX = β1 + β2.GDP + u với EX là xuất khẩu, GDP là tổng sản phẩm quốc nội
(e) GDP = β1 + β2.FDI + u với FDI là đầu tư trực tiếp nước ngoài
(f) EX = β1 + β2.USD + u với USD là giá đồng đôla (VND / 1USD)
(g) M = β1 + β2.R + u với M là cầu về tiền mặt, R là lãi suất
Bài tập 1.3
Cho số liệu mẫu với X là Thu nhập, Y là Chi tiêu của 10 hộ gia đình (đơn vị: triệu đồng) và đồ thị điểm của Chi tiêu theo Thu nhập
Bảng 1.3 a: Số liệu Y và X
Bảng 1.3 a: Số liệu Y và X
| Quan sát | Thu nhập (X) | Chi tiêu(Y) |
| 1 | 8 | 8 |
| 2 | 10 | 11 |
| 3 | 12 | 11 |
| 4 | 12 | 10 |
| 5 | 14 | 14 |
| 6 | 16 | 15 |
| 7 | 16 | 11 |
| 8 | 18 | 15 |
| 9 | 20 | 14 |
| 10 | 20 | 16 |
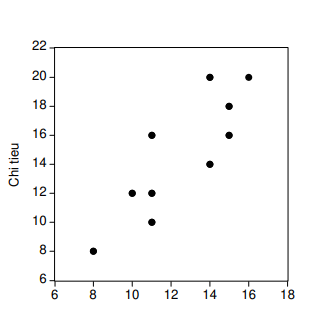
(a) Có thể nói khi thu nhập tăng thì chi tiêu cũng tăng không? Nhận xét gì về xu thế biến động của Chi tiêu theo Thu nhập
(b) Với mô hình hồi quy Y = β1 + β2X + u hãy viết hàm hồi quy tổng thể, công thức chung của hàm hồi quy mẫu, giải thích ý nghĩ các hệ số trong hàm hồi quy
(c) Nêu công thức ước lượng các hệ số β1 và β2 bằng phương pháp bình phương nhỏ nhất OLS
(d) Tính các ước lượng OLS và viết lại hàm hồi quy mẫu với mẫu 10 quan sát qua bảng tính toán 1.3b, và giải thích ý nghĩa kết quả
Bảng 1.3b
| Quan sát | Xi | Yi | xi = Xi - X | yi = Yi - Y | xiyi | xi2 |
| 1 | 8 | 8 | -6.60 | -4.50 | 29.7 | 43.56 |
| 2 | 10 | 11 | -4.60 | -1.50 | 6.9 | 21.16 |
| 3 | 12 | 11 | -2.60 | -1.50 | 3.9 | 6.76 |
| 4 | 12 | 10 | -2.60 | -2.50 | 6.5 | 6.76 |
| 5 | 14 | 14 | -0.60 | 1.50 | -0.9 | 0.36 |
| 6 | 16 | 15 | 1.40 | 2.50 | 3.5 | 1.96 |
| 7 | 16 | 11 | 1.40 | -1.50 | -2.1 | 1.96 |
| 8 | 18 | 15 | 3.40 | 2.50 | 8.5 | 11.56 |
| 9 | 20 | 14 | 5.40 | 1.50 | 8.1 | 29.16 |
| 10 | 20 | 16 | 5.40 | 3.50 | 18.9 | 29.16 |
| Tổng | 146 | 125 | 0.00 | 0.00 | 83 | 152.4 |
| Trung bình | 14.6 | 12.5 |
(e) Qua kết quả trong các câu trên, ước lượng mức chi tiêu trung bình của hộ gia đình khi thu nhập là 24 triệu đồng
(f) Với bảng 1.3c tính các giá trị ước lượng biến phụ thuộc từ hàm hồi quy mẫu Yi và phần dư ei và giải thích ý nghĩa các giá trị đó. Với quan sát thứ 3 thì mức chi tiêu thực tế lớn hơn hay nhỏ hơn mức chi tiêu ước lượng, lớn hơn hay nhỏ hơn bao nhiêu ?
Bảng 1.3c
| Quan sát | Xi | Yi | Y = β1 + β2.Xi | ei = Yi - Yi |
| 1 | 8 | 8 | 8.91 | -0.91 |
| 2 | 10 | 11 | 9.99 | 1.01 |
| 3 | 12 | 11 | 11.08 | -0,08 |
| 4 | 12 | 10 | 11.08 | -1.08 |
| 5 | 14 | 14 | 12.17 | 1.83 |
| 6 | 16 | 15 | 13.26 | 1.74 |
| 7 | 16 | 11 | 13.26 | -2.26 |
| 8 | 18 | 15 | 14.35 | 0.65 |
| 9 | 20 | 14 | 15.44 | -1.44 |
| 10 | 20 | 16 | 15.44 | 0.56 |
| Tổng | 146 | 125 | 125 | 0 |
(g) Từ bảng 1.3b, 1.3c tính được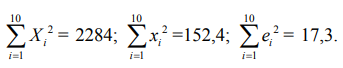 
Hãy tính các đại lượng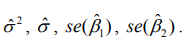 
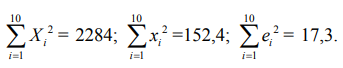Hãy tính các đại lượng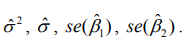 (h) Từ bảng 1.3b, 1.3c tính được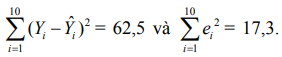 
Hãy tính TSS, ESS, RSS, hệ số xác định R2 và giải thích ý nghĩa của hệ số xác định
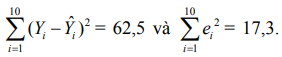Hãy tính TSS, ESS, RSS, hệ số xác định R2 và giải thích ý nghĩa của hệ số xác định(d) Tổng hợp các kết quả tính toán và đối chiếu với kết quả tính toán của Eviews trong bảng 1.3d
Bảng 1.3d
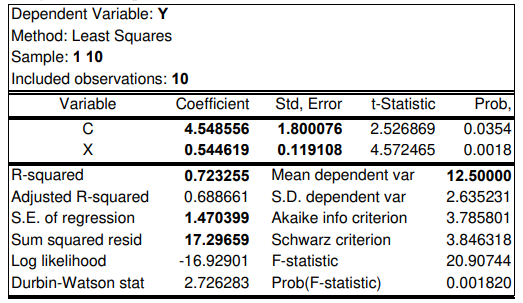
Bài tập 1.4
Cho số liệu 20 đại lý của một hãng bán một loại thịt hộp tại 20 địa điểm tronng một tuần, với P là giá thịt hộp nghìn đồng/hộp, PC là giá bán hàng có tính chất thay thế: cá hộp, nghìn đồng/hộp, Q là sản lượng bán - hộp. Xét mối quan hệ giữa Q và P.
Kết quả ước lượng mô hình Q phụ thuộc bằng Eviews tại bảng 1.4
Bảng 1.4
(a) Viết hàm hồi quy tổng thể, hồi quy mẫu
(b) Giải thích ý nghĩa ước lượng hệ số góc. Dấu các ước lượng hệ số chặn và hệ số góc có phù hợp với lý thuyết kinh tế không ?
(c) Giải thích ý nghĩa hệ số xác định
(d) Các yếu tố khác với giá bán giải thích được bao nhiêu % sự biến động lượng bán ?
(e) Ước lượng điểm lượng bán trung bình khi giá là 31 nghìn đồng
Kết quả ước lượng mô hình Q phụ thuộc bằng Eviews tại bảng 1.4
Bảng 1.4
(a) Viết hàm hồi quy tổng thể, hồi quy mẫu
(b) Giải thích ý nghĩa ước lượng hệ số góc. Dấu các ước lượng hệ số chặn và hệ số góc có phù hợp với lý thuyết kinh tế không ?
(c) Giải thích ý nghĩa hệ số xác định
(d) Các yếu tố khác với giá bán giải thích được bao nhiêu % sự biến động lượng bán ?
(e) Ước lượng điểm lượng bán trung bình khi giá là 31 nghìn đồng
LỜI GIẢI
Bài 1.1 a, b, c, d, e
Bài 1.2
Từ 'trung bình' đi kèm biến phụ thuộc hàm ý đã loại trừ tác động của các yếu tố có tác động tới biến phụ thuộc nhưng không được đưa vào mô hình, nói cách khác là giải thích theo PRF
Hệ số chặn có ý nghĩa cho các mô hình biến độc lập có thể bằng 0
a. β1 - chi tiêu trung bình của hộ gia đình khi không có thu nhập (chi tiêu tự định) β1>0
β2 - chi tiêu trung bình của hộ gia đình khi không có thu nhập (chi tiêu tự định) β2>0
b. Hàng hóa bình thường ⇒ P > 0 ⇒ β1 không cần giải thích ý nghĩa
Ở đây xem xét lượng bán Q như lượng hàng hóa bán được
β2 - mức thay đổi của lượng bán trung bình khi tăng giá thêm 1 đơn vị
β2 < 0 giảm giá thì nhìn chung sẽ bán được nhiếu hơn - cạnh tranh bằng giá
c. β1 - chi phí trung bình cần bỏ ra ngay cả khi chưa sản xuất (chi phí cố định) β1>0
β2 - mức tăng trung bình chi phí khi sản xuất thêm 1 đơn vị sản phẩm (chi tiêu cận biên) β2>0
d. β2 - mức thay đổi của xuất khẩu trung bình GDP tăng thêm 1 đơn vị (chi phí cận biên)
β2>0 - sản xuất trong nước tăng tạo điều kiện tăng xuất khẩu
e. β1 - GDP trung bình khi không nhận thêm vốn đầu tư trực tiếp từ nước ngoài β1>0
β2 - mức thay đổi GDP trung bình khi nhận thêm 1 đơn vị FDI (chi tiêu tự định) β2>0
f. β2 mức thay đổi của xuất khẩu khi giá đồng đô la tăng 1 đơn vị
β2>0 giá đồng đô tăng ⇒ hàng trong nước rẻ hơn tương đối so với hàng nước ngoài ⇒ xuất khẩu nhìn chung tăng
g. Cần tiền - lượng tiền mặt người dân nắm giữ
β1 - cầu tiền trung bình khi lãi suất bằng 0 β1>0
β2 - mức thay đổi của cầu tiền trung bình khi lãi suất tăng 1 đơn vị
β2>0 - lãi suất tăng người dân có xu hướng gửi tiền vào ngân hàng nhiều hơn nên cầu tiền giảm
Bài 1.3
Bài 1.4
Trên đây là toàn bộ tài liệu về 'Bài tập kinh tế lượng chương 1: Mô hình hồi quy tuyến tính hai biến', hi vọng các bạn đã tìm được thông tin mình mong muốn. Đừng quên để lại bình luận dưới bài viết này hoặc phản hồi về fanpage Onthisinhvien.com để được giải đáp sớm nhất nhé.
Chúc bạn học tập hiệu quả - đạt kết quả cao
Xem thêm các bài viết khác
Bài 1.2
Từ 'trung bình' đi kèm biến phụ thuộc hàm ý đã loại trừ tác động của các yếu tố có tác động tới biến phụ thuộc nhưng không được đưa vào mô hình, nói cách khác là giải thích theo PRF
Hệ số chặn có ý nghĩa cho các mô hình biến độc lập có thể bằng 0
a. β1 - chi tiêu trung bình của hộ gia đình khi không có thu nhập (chi tiêu tự định) β1>0
β2 - chi tiêu trung bình của hộ gia đình khi không có thu nhập (chi tiêu tự định) β2>0
b. Hàng hóa bình thường ⇒ P > 0 ⇒ β1 không cần giải thích ý nghĩa
Ở đây xem xét lượng bán Q như lượng hàng hóa bán được
β2 - mức thay đổi của lượng bán trung bình khi tăng giá thêm 1 đơn vị
β2 < 0 giảm giá thì nhìn chung sẽ bán được nhiếu hơn - cạnh tranh bằng giá
c. β1 - chi phí trung bình cần bỏ ra ngay cả khi chưa sản xuất (chi phí cố định) β1>0
β2 - mức tăng trung bình chi phí khi sản xuất thêm 1 đơn vị sản phẩm (chi tiêu cận biên) β2>0
d. β2 - mức thay đổi của xuất khẩu trung bình GDP tăng thêm 1 đơn vị (chi phí cận biên)
β2>0 - sản xuất trong nước tăng tạo điều kiện tăng xuất khẩu
e. β1 - GDP trung bình khi không nhận thêm vốn đầu tư trực tiếp từ nước ngoài β1>0
β2 - mức thay đổi GDP trung bình khi nhận thêm 1 đơn vị FDI (chi tiêu tự định) β2>0
f. β2 mức thay đổi của xuất khẩu khi giá đồng đô la tăng 1 đơn vị
β2>0 giá đồng đô tăng ⇒ hàng trong nước rẻ hơn tương đối so với hàng nước ngoài ⇒ xuất khẩu nhìn chung tăng
g. Cần tiền - lượng tiền mặt người dân nắm giữ
β1 - cầu tiền trung bình khi lãi suất bằng 0 β1>0
β2 - mức thay đổi của cầu tiền trung bình khi lãi suất tăng 1 đơn vị
β2>0 - lãi suất tăng người dân có xu hướng gửi tiền vào ngân hàng nhiều hơn nên cầu tiền giảm
Bài 1.3
Bài 1.4
Trên đây là toàn bộ tài liệu về 'Bài tập kinh tế lượng chương 1: Mô hình hồi quy tuyến tính hai biến', hi vọng các bạn đã tìm được thông tin mình mong muốn. Đừng quên để lại bình luận dưới bài viết này hoặc phản hồi về fanpage Onthisinhvien.com để được giải đáp sớm nhất nhé.
Chúc bạn học tập hiệu quả - đạt kết quả cao
Xem thêm các bài viết khác