Tóm tắt công thức kinh tế lượng
Tóm tắt công thức kinh tế lượng

Đọc bảng kết quả Eviews
|
Dependent Variable: Y |
||||
|
Method: Least Squares |
||||
|
Sample(adjusted): 1 12 |
||||
|
Included observations: 12 after adjusting endpoints |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
32.27726 |
6.253073 |
5.161823 |
0.0006 |
|
X2 |
2.505729 |
0.328573 |
7.626105 |
0.0000 |
|
X3 |
4.758693 |
0.410384 |
11.59572 |
0.0000 |
|
R-squared |
0.975657 |
Mean dependent var |
141.3333 |
|
|
Adjusted R-squared |
0.970247 |
S.D. dependent var |
23.20789 |
|
|
S.E. of regression |
4.003151 |
Akaike info criterion |
5.824358 |
|
|
Sum squared resid |
144.2269 |
Schwarz criterion |
5.945585 |
|
|
Log likelihood |
-31.94615 |
F-statistic |
180.3545 |
|
|
Durbin-Watson stat |
2.527238 |
Prob(F-statistic) |
0.000000 |
|
|
Tiếng Anh |
Ý nghĩa |
|
Dependent Variable: Y |
Biến phụ thuộc: Y |
|
Method: Least Squares |
Phương pháp: Bình phương nhỏ nhất |
|
Sample (adjusted): 1 10 |
Mẫu (sau điều chỉnh): từ 1 đến 10 (loại số liệu) |
|
Included observations: 10 |
Số quan sát được sử dụng: n=10 |
|
Variable |
Biến số (các biến độc lập) |
|
C |
Biến hằng số, C º const |
|
X |
Biến độc lập X |
|
Coefficient |
Ước lượng hệ số: bˆj |
|
Std. Error |
Sai số chuẩn của ước lượng hệ số: Se(bˆj ) |
|
t-Statistic |
Thống kê T: Tqs = bˆj / Se(bˆj ) |
|
Prob. |
Mức xác suất (P-value) của cặp giả thuyết |
|
R-squared |
Hệ số xác định (bội): R2 |
|
Adjusted R-squared |
|
|
S.E. of regression |
Sai số chuẩn của hồi quy: sˆ |
|
Sum squared resid |
Tổng bình phương phần dư: RSS |
|
Durbin-Watson stat |
Thống kê Durbin-Watson:d |
|
Mean dependent var |
|
|
S.D. dependent var |
Độ lệch chuẩn biến phụ thuộc: SY= căn ( TTS/ ( n-1)) |
|
F-statistic |
2 |
|
Prob (F-statistic) |
Mức xác suất (P-value) của kiểm định sự phù hợp hàm hồi quy |
DẠNG 1: XÂY DỰNG MÔ HÌNH HỒI QUY KINH TẾ LƯỢNG
1.1. Các câu hỏi thường gặp
- Xây dựng mô hình hồi quy phù hợp với yêu cầu.
- Hiệu chỉnh mô hình để phù hợp với lý thuyết hoặc thực tế: thêm biến, bỏ biến, đổi dạng hàm.
- Dự báo (ước lượng) giá trị biến phụ thuộc 𝑌̂ hoặc sự thay đổi của biến phụ thuộc ∆𝑌.
- Giải thích ý nghĩa kinh tế của các hệ số (ước lượng) hoặc giải thích các hệ số đặc biệt.
- Dấu hệ số như nào là phù hợp hoặc dấu hệ số ước lượng có phù hợp lý thuyết kinh tế không?
1.2. Lý thuyết cần nhớ
Các dạng hàm hồi quy và ý nghĩa kinh tế của các hệ số
- Hàm hồi quy tuyến tính bội
𝑌𝑖 = 𝛽1 + 𝛽2. 𝑋2𝑖 + 𝛽3. 𝑋3𝑖 + ⋯ + 𝛽𝑘. 𝑋𝑘𝑖 + 𝑢𝑖
𝛽1(hệ số chặn): cho biết khi tất cả các biến độc lập cùng bằng 0 thì trung bình biến phụ thuộc là 𝛽1
đơn vị.
𝛽𝑚(hệ số góc): cho biết khi biến độc lập Xm tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc thay đổi |𝜷𝒎| đơn vị, với điều kiện các yếu tố khác không đổi.
- Hàm hồi quy đa thức (parabol)
𝑌𝑖 = 𝛽1 + 𝛽2. 𝑋𝑖 + 𝛽3. 𝑋𝑖2 + 𝑢𝑖
𝛽1(hệ số chặn): cho biết khi biến độc lập X bằng 0 thì trung bình biến phụ thuộc là 𝛽1 đơn vị.
+) Xét dấu hệ số 𝛽3 (vẽ đồ thị): 𝛽3 > 0 có cực tiểu, 𝛽3 < 0 có cực đại.
Mối quan hệ X-Y: 𝛽3 > 0 thì ban đầu X tăng Y giảm rồi sau đó X tăng Y tăng, 𝛽3 < 0 thì ban đầu X tăng Y tăng rồi sau đó X tăng Y giảm.
+) Tại điểm X0 cụ thể: 𝑌x0, = 𝛽2 + 2𝛽3. 𝑋0 = 𝑎
Cho biết tại điểm X0, khi X tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc thay đổi |𝒂| đơn vị.
+) Điểm cực trị: 𝑋∗ =
- Hàm hồi quy đa thứ (tương tác biến định lượng)
𝑌𝑖 = 𝛽1 + 𝛽2. 𝑋𝑖 + 𝛽3. 𝑍𝑖 + 𝛽4. 𝑋𝑖 ∗ 𝑍𝑖 + 𝑢𝑖
𝛽1(hệ số chặn): cho biết khi biến độc lập X=Z=0 thì trung bình biến phụ thuộc là 𝛽1 đơn vị.
𝛽2(hệ số góc): cho biết khi biến độc lập X tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc thay đổi
|𝜷𝟐| đơn vị, với điều kiện các yếu tố khác =0.
𝛽3(hệ số góc): cho biết khi biến độc lập Z tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc thay đổi
|𝜷𝟑| đơn vị, với điều kiện các yếu tố khác =0.
𝛽4(hệ số góc): cho biết tác động của X đến Y phụ thuộc vào độ lớn của Z và tác động của Z đến Y phụ thuộc độ lớn của X.
- Hàm hồi quy nghịch đảo (hypecbol)
𝑌𝑖 = 𝛽1 + 𝛽2/𝑋𝑖 + 𝑢𝑖
+) Xét dấu hệ số 𝛽2 (vẽ đồ thị): 𝛽2 > 0 thì trung bình biến phụ thuộc đạt cực tiểu là 𝛽1 đơn vị, 𝛽2 < 0 thì trung bình biến phụ thuộc đạt cực đại là 𝛽1 đơn vị.
+) Mối quan hệ X-Y: 𝛽2 > 0 thì X tăng Y giảm, 𝛽2 < 0 thì X tăng Y tăng.
- Hàm hồi quy loga tuyến tính (hàm mũ, điển hình là hàm sản xuất Cobb-Douglas)
𝑙𝑜𝑔𝑌𝑖 = 𝛽1 + 𝛽2. 𝑙𝑜𝑔𝑋𝑖 + 𝑢𝑖
𝛽1(hệ số chặn): cho biết khi biến độc lập cùng bằng 1 đơn vị thì trung bình biến phụ thuộc là 𝑒𝛽1đơn vị.
𝛽2(hệ số góc): cho biết khi biến độc lập X tăng (giảm) 1 % thì trung bình biến phụ thuộc thay đổi
|𝛽𝟐| %, với điều kiện các yếu tố khác không đổi.
- Hàm hồi quy semi-loga
𝑙𝑜𝑔𝑌𝑖 = 𝛽1 + 𝛽2. 𝑋𝑖 + 𝑢𝑖
𝑌𝑖 = 𝑒𝛽1+𝛽2.𝑋𝑖+𝑢𝑖
𝛽1(hệ số chặn): cho biết khi biến độc lập bằng 0 thì trung bình biến phụ thuộc là 𝑒𝛽1 đơn vị.
𝛽2(hệ số góc): cho biết khi biến độc lập X tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc thay đổi
|𝛽𝟐| × 𝟏𝟎𝟎%.
𝑌𝑖 = 𝛽1 + 𝛽2. 𝑙𝑜𝑔𝑋𝑖 + 𝑢𝑖
𝛽1(hệ số chặn): cho biết khi biến độc lập bằng 1 đơn vị thì trung bình biến phụ thuộc là 𝛽1 đơn vị.
𝛽2(hệ số góc): cho biết khi biến độc lập X tăng (giảm) 1 % thì trung bình biến phụ thuộc thay đổi
|𝛽𝟐|/𝟏𝟎𝟎 đơn vị.
- Hàm hồi quy có biến giả (vẽ đồ thị các trường hợp chênh lệch hệ số chặn, hệ số góc hoặc cả hai)
𝑌𝑖 = 𝛽1 + 𝛽2. 𝑋𝑖 + 𝛽3. 𝐷 + 𝑢𝑖
𝛽1(hệ số chặn): cho biết khi biến độc lập bằng 0 thì trung bình biến phụ thuộc ở trạng thái D=0 là 𝛽1
đơn vị.
𝛽2(hệ số góc): cho biết khi biến độc lập X tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc thay đổi
|𝛽𝟐| đơn vị.
𝛽3(hệ số góc): cho biết ở các mức X tương ứng thì trung bình biến phụ thuộc ở trạng thái D=1 chênh lệch so với trạng thái D=0 là |𝖰𝟑| đơn vị.
𝑌𝑖 = 𝛽1 + 𝛽2. 𝑋𝑖 + 𝛽4. 𝐷𝑋𝑖 + 𝑢𝑖
𝛽1(hệ số chặn): cho biết khi biến độc lập bằng 0 thì trung bình biến phụ thuộc là 𝛽1 đơn vị.
𝛽2(hệ số góc): cho biết khi biến độc lập X tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc ở trạng thái D=0 thay đổi |𝛽𝟐| đơn vị.
𝛽4(hệ số góc): cho biết khi X tăng (giảm) 1 đơn vị thì mức thay đổi trung bình biến phụ thuộc ở trạng thái D=1 chênh lệch so với trạng thái D=0 là |𝛽𝟒| đơn vị.
- Hàm hồi quy trễ phân phối
𝑌𝑡 = 𝛼 + 𝛽0. 𝑋𝑡 + 𝛽1. 𝑋𝑡−1 + 𝛽2. 𝑋𝑡−2 + ⋯ + 𝛽𝑝. 𝑋𝑡−𝑝 + 𝑢𝑡
𝛼 (hệ số chặn): cho biết khi biến độc lập ở các thời kỳ cùng bằng 0 thì trung bình biến phụ thuộc là
𝛼 đơn vị.
𝛽0(hệ số góc): cho biết khi biến độc lập X hiện tại tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc ở thời điểm hiện tại thay đổi |𝖰𝟎| đơn vị.
𝛽1(hệ số góc): cho biết khi biến độc lập X trước đó 1 thời kỳ tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc ở thời điểm hiện tại thay đổi |𝖰𝟏| đơn vị, với điều kiện các yếu tố khác không đổi.
cho biết khi biến độc lập X hiện tại tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc ở sau đó 1 thời kỳ thay đổi |𝖰𝟏| đơn vị, với điều kiện các yếu tố khác không đổi.
- Hàm hồi quy có xu thế
𝑌𝑡 = 𝛽1 + 𝛽2. 𝑋𝑡 + 𝛽3. 𝑇 + 𝑢𝑡
𝛽1(hệ số chặn): cho biết khi biến độc lập bằng 0 ở thời điểm gốc (T=0) thì trung bình biến phụ thuộc là 𝛽1 đơn vị (lưu ý trường hợp cho T=1 là gốc)
𝛽2(hệ số góc): cho biết khi biến độc lập X tăng (giảm) 1 đơn vị thì trung bình biến phụ thuộc ở thời điểm hiện tại thay đổi |𝖰𝟐| đơn vị.
𝛽3(hệ số góc): cho biết cứ sau 1 thời kỳ thì trung bình biến phụ thuộc có xu thế thay đổi |𝖰𝟑| đơn vị, với điều kiện các yếu tố khác không đổi.
* Yêu cầu:
- Viết lại hàm hồi quy tổng thể, hàm và mô hình hồi quy mẫu cho các dạng hàm trên.
- Tự vẽ lại đồ thị các dạng hàm đa thức (parabol, hypecbol và có biến giả).
- Tìm các lý thuyết kinh tế (vi mô + vĩ mô) áp dụng các dạng hàm trên (ví dụ: hàm cầu dùng dạng tuyến tính, hàm sản xuất dùng dạng Cobb-Douglas, hàm tổng chi phí dùng dạng đa thức,…)
DẠNG 2: SUY DIỄN THỐNG KÊ
2.1. Các câu hỏi thường gặp
- Các hệ số có ý nghĩa thống kê không?
- Phân tích mối quan hệ biến độc lập và biến phụ thuộc.
- Ước lượng/ Kiểm định sự thay đổi biến phụ thuộc khi biến độc lập thay đổi-Hàm Cobb-Douglas: hàm sản xuất thay đổi theo quy mô…
2.2. Lý thuyết cần nhớ
Bước 1: Xác định hệ số cần ước lượng/ kiểm định (xem lại ý nghĩa kinh tế các hệ số)
- Hệ số riêng 𝛽𝑗
- Hệ số đồng thời 𝛽 = 𝑎𝛽𝑖 ± 𝑏𝛽𝑗
(cách tính 𝛽̂, 𝑠𝑒(𝛽̂))
Khoảng thay đổi của Y khi 2 biến thay đổi:
|
Mức thay đổi Xi |
Mức thay đổi Xj |
Mức thay đổi Y |
|
Tăng a |
Tăng b |
|
|
Tăng a |
Giảm b |
|
|
Giảm a |
Tăng b |
|
|
Giảm a |
Giảm b |
Bước 2: Xác định bài toán ước lượng:
- Khoảng nào? à KTC đối xứng
- Tối đa à Tối đa (nếu là hệ số chặn /hệ số góc 𝛽̂ > 0), Tối thiểu (nếu hệ số góc 𝛽̂ < 0)
- Tối thiểu à Tối thiểu (nếu là hệ số chặn/hệ số góc 𝛽̂ > 0), Tối đa (nếu hệ số góc 𝛽̂ < 0)
Công thức khoảng tin cậy của hệ số:
KTC đối xứng: KTC tối đa:
KTC tối thiểu:
Bước 3: Xác định bài toán kiểm định (suy luận với |𝛽̂| và |𝛽|)
- Viết cặp kiểm định giả thuyết:
- Có dấu bằng (=, ≤, ≥) là H0
- Không có dấu bằng (≠, >, < ) là H1
- H0, H1 là hai giả thuyết đối nhau
- Tiêu chuẩn kiểm định Tà Tqs
- Miền bác bỏ 𝑊𝛼
- Kết luận: 𝑇𝑞𝑠 ∈ 𝑊𝛼: bác bỏ H0
𝑇𝑞𝑠 ∉ 𝑊𝛼: chưa có cơ sở bác bỏ H0
|
Kiểm định |
Tiêu chuẩn |
Miền bác bỏ |
|
𝐻0: 𝛽 = 𝛽∗ |
|
𝑊 = {𝑇: |𝑇| > 𝑡(𝑛−𝑘)} |
|
𝐻0: 𝛽 ≥ 𝛽∗ |
𝑊 = {𝑇: 𝑇 < −𝑡(𝑛−𝑘)} |
|
|
𝐻0: 𝛽 ≤ 𝛽∗ |
𝑊 = {𝑇: 𝑇 > 𝑡(𝑛−𝑘)} |
- Hệ số có ý nghĩa thống kê (sử dụng p –value)
𝐻0: 𝛽𝑗 = 0
{𝐻1: 𝛽𝑗 ≠ 0
- Mối quan hệ X-Y
|
𝐻0: 𝛽𝑗 = 0 |
𝐻0: 𝛽𝑗 ≤ 0 |
𝐻0: 𝛽𝑗 ≥ 0 |
- Mức độ tác động của 2 biến độc lập lên biến phụ thuộc (xét 2 hệ số góc cùng hay khác dấu)
|
𝐻0: |𝛽𝑖| = |𝛽𝑗| |
𝐻0: |𝛽𝑖| ≤ |𝛽𝑗| |
𝐻0: |𝛽𝑖| ≥ |𝛽𝑗| |
- Hàm Cobb-Douglas: hàm sản xuất thay đổi theo quy mô
|
𝐻0: 𝛽2 + 𝛽3 = 1 |
{𝐻0: 𝛽2 + 𝛽3 ≤ 1 |
{𝐻0: 𝛽2 + 𝛽3 ≥ 1 |
- Hàm có biến giả: hàm hồi quy đồng nhất
|
{𝐻0: 𝛽3 = 0 |
𝐻0: 𝛽4 = 0 |
{𝐻0: 𝛽3 = 𝛽4 = 0 |
- Hàm có biến xu thế: lưu ý đơn vị thời gian (theo năm, tháng hay quý) và thời điểm (quá khứ, hiện tại, tương lai).
DẠNG 3: PHÂN TÍCH HÀM HỒI QUY
3.1. Các câu hỏi thường gặp
- Ý nghĩa hệ số xác định R2
- Kiểm định sự phù hợp của hàm hồi quy (các biến độc lập đều không ảnh hưởng đến biến phụ thuộc)
- Kiểm định thêm biến, bỏ biến
3.2. Lý thuyết cần nhớ
- Ý nghĩa hệ số xác định: Cho biết hàm hồi quy (hoặc các biến độc lập) giải thích được R2×100% sự thay đổi của biến phụ thuộc, phần còn lại (1- R2) ×100% là do các yếu tố khác ngoài các biến độc lập hay yếu tố ngẫu nhiên gây ra.
- Kiểm định sự phù hợp hàm hồi quy:
|
Cách 1: sử dụng miền bác bỏ |
Cách 2: sử dụng p-value
|
- Kiểm định thêm biến, bỏ biến:
Xác định mô hình lớn (có nhiều biến), mô hình nhỏ (có ít biến) Cặp kiểm định tương ứng (theo các hệ số thêm vào hoặc bớt đi)
Tiêu chuẩn kiểm định:
Miền bác bỏ 𝑊 :
− 𝐹𝑞𝑠 ∈ 𝑊𝛼: bác bỏ
− 𝐹𝑞𝑠 ∉ 𝑊𝛼: chưa có cơ sở bác bỏ H0
* Lưu ý: ứng dụng kiểm định bỏ biến cho kiểm định với hàm có biến giả (hàm hồi quy đồng nhất, kiểm định biến X hoặc D có ảnh hưởng đến Y)
DẠNG 4: ĐÁNH GIÁ MÔ HÌNH
4.1. Các câu hỏi thường gặp
- Nguyên nhân, bản chất, hậu quả của các khuyết tật gây ra cho mô hình, đề xuất biện pháp khắc phục (nếu có khuyết tật)
- Đánh giá mô hình (phát hiện khuyết tật) và nêu phương pháp thực hiện kiểm định.
- So sánh các mô hình để chọn ra mô hình tốt nhất
4.2. Lý thuyết cần nhớ
|
TT |
Giả thiết OLS |
Vi phạm |
Khuyết tật |
Hậu quả |
Phát hiện |
Khắc phục |
Lưu ý |
|
1 |
𝑬(𝑼⁄𝑿) = 𝟎 |
𝑬(𝑼⁄𝑿) ≠ 𝟎 |
Định dạng hàm sai (Mô hình thiếu biến) |
- Ước lượng OLS bị chệch |
Kiểm định Ramsey |
- Thêm biến |
Gây hậu quả nghiêm trọng nhất |
|
2 |
𝒗𝒂𝒓(𝑼⁄𝑿) ≡ 𝝈𝟐 |
𝒗𝒂𝒓(𝑼⁄𝑿) |
Phương sai sai số thay đổi |
|
Kiểm định White |
quát GLS |
Hay xảy ra với số liệu chéo |
|
3 |
𝑼~𝑵(𝟎, 𝝈𝟐) |
𝑼 ≁ 𝑵(𝟎, 𝝈𝟐) |
Sai số ngẫu nhiên không phân phối chuẩn |
suy diễn thống kê không đáng tin cậy |
Kiểm định JB |
- Tăng kích thước mẫu |
Gây ít hậu quả nhất, không có |
|
4 |
𝒄𝒐𝒗(𝑿𝒊, 𝑿𝒋) = 𝟎 |
𝒄𝒐𝒗(𝑿𝒊, 𝑿𝒋) |
Đa cộng tuyến |
* Tuy nhiên đây vẫn là ước lượng tuyến tính không |
Hồi quy |
|
Chỉ xảy ra với mô |
|
5 |
|
|
Tự tương quan |
|
Kiểm định DW |
phân tổng quát
Orcutt |
Hay xảy ra với số liệu chuỗi (số |
Kết quả ước lượng bằng Eviews
|
Dependent Variable: Y |
||||
|
Method: Least Squares |
||||
|
Sample(adjusted): 1 12 |
||||
|
Included observations: 12 after adjusting endpoints |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
32.27726 |
6.253073 |
5.161823 |
0.0006 |
|
X2 |
2.505729 |
0.328573 |
7.626105 |
0.0000 |
|
X3 |
4.758693 |
0.410384 |
11.59572 |
0.0000 |
|
R-squared |
0.975657 |
Mean dependent var |
141.3333 |
|
|
Adjusted R-squared |
0.970247 |
S.D. dependent var |
23.20789 |
|
|
S.E. of regression |
4.003151 |
Akaike info criterion |
5.824358 |
|
|
Sum squared resid |
144.2269 |
Schwarz criterion |
5.945585 |
|
|
Log likelihood |
-31.94615 |
F-statistic |
180.3545 |
|
|
Durbin-Watson stat |
2.527238 |
Prob(F-statistic) |
0.000000 |
|
1.Kiểm định dạng hàm bằng kiểm định Ramsey RESET
|
Ramsey RESET Test: number of fitted term: 1 |
||||
|
F-statistic |
0.434041 |
Probability |
0.528515 |
|
|
Log likelihood ratio |
0.634014 |
Probability |
0.425887 |
|
|
|
||||
|
Dependent Variable: Y Included observations: 12 |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
15.89090 |
25.69746 |
0.618384 |
0.5535 |
|
X2 |
3.676299 |
1.808903 |
2.032337 |
0.0766 |
|
X3 |
6.810923 |
3.143733 |
2.166508 |
0.0622 |
|
FITTED^2 |
-0.001588 |
0.002410 |
-0.658818 |
0.5285 |
|
R-squared |
0.976909 |
F-statistic |
112.8200 |
|
|
Durbin-Watson stat |
2.805915 |
Prob(F-statistic) |
0.000001 |
|
2. Kiểm định hiện tượng phương sai sai số thay đổi bằng kiểm định White
|
White Heteroskedasticity Test: cross term |
||||
|
F-statistic |
0.843820 |
Probability |
0.564521 |
|
|
Obs*R-squared |
4.954369 |
Probability |
0.421474 |
|
|
Test Equation: |
||||
|
Dependent Variable: RESID^2 Included observations: 12 |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
-302.2919 |
201.0729 |
-1.503394 |
0.1834 |
|
X2 |
31.71005 |
20.36090 |
1.557400 |
0.1704 |
|
X2^2 |
-0.879882 |
0.520465 |
-1.690568 |
0.1419 |
|
X2*X3 |
0.206625 |
0.536312 |
0.385270 |
0.7133 |
|
X3 |
0.587451 |
10.18193 |
0.057695 |
0.9559 |
|
X3^2 |
-0.075395 |
0.534322 |
-0.141104 |
0.8924 |
|
R-squared |
0.412864 |
F-statistic |
0.843820 |
|
|
Durbin-Watson stat |
2.579780 |
Prob(F-statistic) |
0.564521 |
|
3.Kiểm định hiện tượng sai số ngẫu nhiên phân phối chuẩn bằng kiểm định Jarque-Bera
|
Normality Test: |
|||
|
JB |
0.985686 |
Probability |
0.349875 |
|
Dependent Variable: X2 |
||||
|
Included observations: 12 after adjusting endpoints |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
13.11995 |
4.359437 |
3.009550 |
0.0131 |
|
X3 |
0.599730 |
0.346453 |
1.731059 |
0.1141 |
|
R-squared |
0.230566 |
F-statistic |
2.996565 |
|
|
Durbin-Watson stat |
1.684565 |
Prob(F-statistic) |
0.114120 |
|
|
Dependent Variable: X3 |
||||
|
Included observations: 12 after adjusting endpoints |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
4.317495 |
4.620929 |
0.934335 |
0.3721 |
|
X2 |
0.384449 |
0.222089 |
1.731059 |
0.1141 |
|
R-squared |
0.230566 |
F-statistic |
2.996565 |
|
|
Durbin-Watson stat |
1.819293 |
Prob(F-statistic) |
0.114120 |
|
5.a.Kiểm định hiện tượng tự tương quan bằng kiểm định Durbin-Watson
Với α = 5%, kích thước mẫu = n và số biến giải thích là k’ = k-1:
Durbin – Watson đã xây dựng bảng các giá trị cận dưới d (Lower), cận trên d (Upper) để làm căn cứ
kết luận.
0 ---------------- dL--------- dU ------------- 4-dU ---------- 4-dL--------------------- 4
5.b.Kiểm định hiện tượng tự tương quan bằng kiểm định Breusch-Godfrey
|
Breusch-Godfrey Serial Correlation LM Test: AR(1) |
||||
|
F-statistic |
0.985686 |
Probability |
0.349875 |
|
|
Obs*R-squared |
1.316342 |
Probability |
0.251250 |
|
|
Test Equation: |
||||
|
Presample missing value lagged residuals set to zero. |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
-0.801269 |
6.309879 |
-0.126986 |
0.9021 |
|
X2 |
0.038385 |
0.331099 |
0.115931 |
0.9106 |
|
X3 |
0.009196 |
0.410815 |
0.022385 |
0.9827 |
|
RESID(-1) |
-0.348885 |
0.351409 |
-0.992817 |
0.3499 |
|
R-squared |
0.109695 |
F-statistic |
0.328562 |
|
|
Durbin-Watson stat |
1.853452 |
Prob(F-statistic) |
0.805069 |
|
*Cách thực hiện kiểm định các khuyết tật theo ví dụ trên:
Mô hình gốc: ${{\gamma }_{i}}={{\beta }_{1}}+{{\beta }_{2}}.{{X}_{2i}}+{{\beta }_{3}}.{{X}_{3i}}+{{u}_{i}}$
- Với số quan sát: n, số hệ số: k, hệ số xác định ${{R}^{2}}$
- Bước 1: Ước lượng mô hình gốc thu được $\overset{\wedge }{\mathop{\gamma }}\,$
- Bước 2: xây dựng mô hình hồi quy phụ
***REPAIRED***
- Bước 3: Kiểm định khuyết tật
Tiêu chuẩn kiểm định:$F=\frac{(R_{P}^{2}-{{R}^{2}})/m}{(1-R_{P}^{2})/(n-k-m)}$
Miền bác bỏ ${{W}_{\alpha }}:{{W}_{\alpha }}=\left\{ F:F>f_{\alpha }^{(m.n-k-m)}\left. {} \right\} \right.$
Lưu ý: số nhâm tử thêm vào (number of fitted)
Khuyết tật 2: Phương sai sai số thay đổi
- Bước 1: Ước lượng mô hình gốc thu được
- Bước 2: Xây dựng mô hình hồi quy phụ (cross-có tích chéo)
Xây dựng mô hình hồi quy phụ (no cross – không có tích chéo)
$e_{i}^{2}={{\alpha }_{1}}+{{\alpha }_{2}}.{{X}_{2i}}+{{\alpha }_{3}}.{{X}_{3i}}+{{\alpha }_{4}}.X_{2i}^{2}+{{\alpha }_{5}}.X_{3i}^{2}+{{v}_{i}}(P)$
- Bước 3: kiểm định khuyết tật

- Tiêu chuẩn kiểm định: $F=\frac{R_{P}^{2}/(m-1)}{(1-R_{P}^{2})/(n-m)}$
- Miền bác bỏ ${{W}_{\alpha }}:{{W}_{\alpha }}=\left\{ F:F>f_{\alpha }^{(m-1,n-m} \right\}$
- Tiêu chuẩn kiểm định: ${{X}^{2}}=n.R_{P}^{2}$
- Miền bác bỏ ${{W}_{\alpha }}:{{W}_{\alpha }}=\left\{ {{X}^{2}}:{{X}^{2}}>X_{\alpha }^{{{2}^{(m)}}} \right\}$
Khuyết tật 3: sai số nẫu nhiên không phân phối chuẩn
- Bước 1: Ước lượng mô hình gốc thu được phần dư e rồi tính hệ số bất đối xứng S, hệ số nhọn K
- Bước 2: Kiểm định khuyết tật

Tiêu chuẩn kiểm định:${{\chi }^{2}}=n.(\frac{{{S}^{2}}}{6}+\frac{{{(K-3)}^{2}}}{24})$
Miền bác bỏ: ${{W}_{\alpha }}:{{W}_{\alpha }}=\left\{ {{\chi }^{2}}:{{\chi }^{2}}>\chi _{\alpha }^{2(2)} \right\}$
Khuyết tật 4: Đa cộng tuyến
- Bước 1: Xây dựng mô hình hồi quy phụ
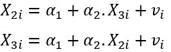
- Bước 2: kiểm định khuyết tật
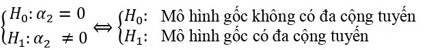
Khuyết tật 5: Tự tương quan (BG)
- Bước 1: Ước lượng mô hình gốc thu được phần dư e và các trễ của nó
- Bước 2: Xây dựng mô hình hồi quy phụ
$\begin{align}
& {{e}_{t}}=({{\beta }_{1}}+{{\beta }_{2}}.{{X}_{2t}}+{{\beta }_{3}}.{{X}_{3t}})+{{p}_{1}}.{{e}_{t-1}}+...+{{p}_{p}}.{{e}_{t-p}}+{{v}_{t}}\left( L \right) \\
& {{e}_{t}}=({{\beta }_{1}}+{{\beta }_{2}}.{{X}_{2t}}+{{\beta }_{3}}.{{X}_{3t}})+{{v}_{t}}\left( N \right) \\
\end{align}$
- Bước 3: Kiểm định khuyết tật
Miền bác bỏ ${{W}_{\alpha }}:{{W}_{\alpha }}=\left\{ F:F>f_{\alpha }^{(p,n-k-p)} \right\}$
Tiêu chuẩn kiểm định: ${{X}^{2}}=n.R_{L}^{2}$
Miền bác bỏ ${{W}_{\alpha }}:{{W}_{\alpha }}=\left\{ {{X}^{2}}:{{X}^{2}}>X_{\alpha }^{2(p)} \right\}$
Lưu ý: Bậc tự tương quan kiểm định AR(p), số hệ số trong hồi quy phụ là (k+p), số quan sát theo lý thuyết là (n-p) nhưng phần mềm tự thay bằng giá trị 0 nên số quan sát thực tế là n.
*Quan trọng:
1. Cặp kiểm định chung cho phần kiểm định các khuyết tật
- Sử dụng p-value để nhận xét mô hình có khuyết tật không?
p-value <
p-value >
2. Quy tắc lựa chọn mô hình tốt nhất
- Số khuyết tạt mắc phải càng ít càng tốt
- Hậu quả khuyết tật gay ra: hậu quả càng ít nghiêm trọng càng tốt
- Dạng hàm sử dụng: dạng hàm càng phong phú, càng phù hợp lý thuyết càng tốt
- Nếu cùng biến phụ thuộc Y thì có thể so sánh hệ số xác định R2: R2 càng cao càng tốt (lưu ý: biến phụ thuộc Y
Tổng kết công thức kinh tế lượng





Ôn thi sinh viên là hình thức học tập mới, cung cấp cho tất cả sinh viên giảng đường thứ 2 cung cấp kiến thức để mọi người có thể tự học tập và nghiên cứu.
Hệ thống sẽ dựa trên kiến thức của từng trường đại học cùng với các bạn sinh viên xây dựng những bài giảng, bài thi phù hợp với thực tiễn học tập của sinh viên các trường. Các bài tập sẽ được phân loại theo từng phần => dễ học hơn, dễ nắm bắt được kiến thức hơn, biết được phần này sẽ học những dạng bài nào, cách giải chúng nó ra sao. Mất gốc cũng học được nha! Mỗi dạng bài tập luôn được giải chi tiết và mang văn phong "hướng dẫn" => Giải thích cho bạn hiểu tại sao lại ra đáp án này, tại sao lại dùng công thức này. Điều này sẽ giúp bạn "trơn tru" trong quá trình học tập, không sợ không hiểu tại sao bài này làm kiểu gì nữa. Đề thi mẫu cập nhật mới nhất (có đáp án giải thích chi tiết) => Theo form đề thi thật. Vậy nên hãy ấn link dưới đây nếu bạn đang tìm kiếm trải nghiệm học tập đáng nhớ nhé.
Chúc các bạn may mắn!!!
Đại học kinh tế quốc dân: Bấm vào đây
Học viện tài chính: Bấm vào đây
 Liên hệ tương tác trực tiếp qua zalo: 0359.286.819 (chị Linh - giải quyết khó khăn môn Nguyên lý kế toán, Kế toán tài chính TẤT CẢ CÁC TRƯỜNG ĐẠI HỌC)
Liên hệ tương tác trực tiếp qua zalo: 0359.286.819 (chị Linh - giải quyết khó khăn môn Nguyên lý kế toán, Kế toán tài chính TẤT CẢ CÁC TRƯỜNG ĐẠI HỌC)
💥Giải đáp FREE các câu hỏi về NGUYÊN LÝ KẾ TOÁN
💥Nhận gia sư 1-1 cấp tốc cho người mất gốc (online/offline)
💥Nhận booking giải bài tập về nhà, đề cương ôn tập , làm mẫu các đề thi (có đáp án và giải thích chi tiết)
Đọc chi tiết dịch vụ tại đây
📍 KHÔNG NHẬN THI HỘ - HỌC LÀ HIỂU BẢN CHẤT