Tổng hợp kiến thức thi giữa kỳ môn Xác Suất Thống Kê
Ngày: 25/09/2020
TỔNG HỢP KIẾN THỨC THI GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ
Để các bạn có được sự chuẩn bị tốt nhất cho bài thi giữa kỳ cho môn học này, mình sẽ hệ thống lại kiến thức từ chương 1 tới chương 4 để các bạn có thể dễ dàng hơn trong việc ôn tập và đạt điểm cao.
Chờ gì nữa, bắt đầu thôi !!
I. Chương 1: Chương mở đầu
Chương này chỉ mang tính chất giới thiệu,bạn nào muốn đọc thì đọc, không muốn thì có thể bỏ qua nhé ^^
II. Chương 2: Biến cố và xác suất
Chương này cần nhớ các công thức xác suất biến cố tổng, biến cố tính,xác suất đầy đủ,công thức Bayes,công thức Bernoulli…
Xác suất của biến cố tích
• Với A và B là 2 biến cố độc lập ta có: P(AB) = P(A).P(B)
• Với A và B là 2 biến cố phụ thuộc ta có: P(AB) = P(A/B).P(B) = P(B/A).P(A)
•Với A và B là 2 biến cố xung khắc ta có: P(AB) = 0
Xác suất của biến cố tổng

-Giả sử có n phép thử độc lập
-Trong mỗi phép thử,xác suất để xảy ra biến cố A là như nhau và bằng p, xác suất không xảy ra A là 1 – p
-Xác suất để trong n phép thử đó, biến cố A xảy ra đúng x lần được ký hiệu là P(x | n,p)
-Công thức Bernoulli: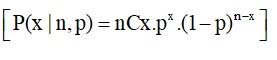
Công thức XS đầy đủ,công thức Bayes
- Cho H1, H2,….., Hn là một nhóm đầy đủ các biến cố

>> Hiểu rõ Xác suất thống kê hơn cùng mentor Viết Duy !!
III. Chương 3: Biến ngẫu nhiên rời rạc
1) Khái niệm:
• Kí hiệu biến ngẫu nhiên: X,Y, Z,.. Giá trị có thể có của X ký hiệu: X1, X2, Xn .
-Một biến được gọi là biến ngẫu nhiên rời rạc nếu các giá trị có thể có của nó lập nên một tập hợp hữu hạn hoặc đếm được.
2) Bảng phân phối xác suất(Chỉ BNN rời rạc mới có)
•Cho biến NN rời rạc X nhận các giá trị x1,x2,…,xn với xác suất tương ứng p1,p2,…pn.
Bảng trên gọi là bảng phân phối xác suất của biến ngẫu nhiên rời rạc X
3)Các tham số đặc trưng
•Kì vọng(trung bình)
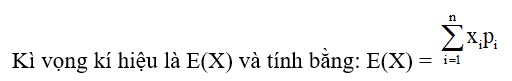
Đơn vị của kì vọng là đơn vị của X
Tính chất:
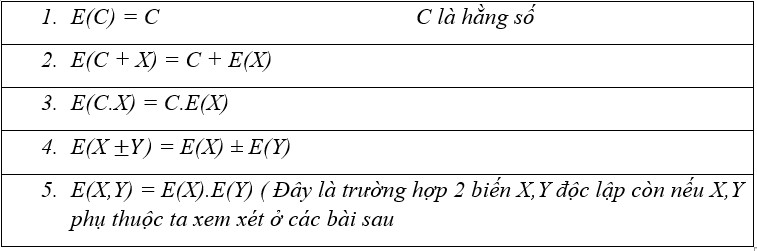
•Phương sai:
-Phương sai phản ảnh độ phân tản của biển ngẫu nhiên. Phương sai lớn thì độ phân tán lớn. Phương sai phản ánh độ rúi ro, độ ổn định, độ đồng đều.

4) Quy luật Phân phối xác suất cho BNN rời rạc
•Quy luật phân phối 0 – 1
Định nghĩa: Biến ngẫu nhiên rời rạc X chỉ nhận một trong hai giá trị hoặc 1 với xác suất được tính bởi công thức
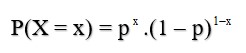
Được gọi là có phân phối 0- 1 với tham số p. Kí hiệu: X ~ A(p)
X có bảng phân phối xác suất
Tham số đặc trưng: E(X) = p: V(X) = p(1 – p)
•Quy luật phân phối Nhị thức
- Xét n phép thử độc lập. Xác suất xảy ra biến cố A trong mỗi phép thử là p. Gọi X là số lần bc A xảy ra,trong n lần thử. X có thể nhận các giá trị 0, 1, 2,..n với các xác suất tương ứng được tính theo công thức

-Các tham số đặc trưng:
• Kỳ vọng E(X) = np • Phương sai V(X) = np(1-p)
• Mốt m0: np + p -1 ≤ m0 ≤ np + p

•PHÂN PHỐI POISSON
Định nghĩa: Biến ngẫu nhiên rời rạc X nhận một trong các giá trị có thể có là 0, 1, 2, .. với các xác suất tương ứng được tính theo công thức :
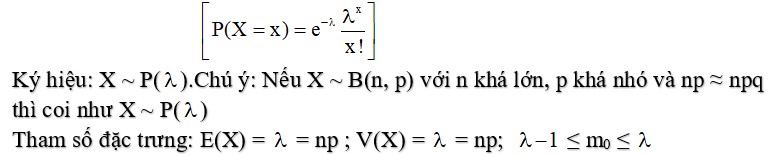
>> Thi thử ngay với bộ ngân hàng đề 1000 câu hỏi
IV. Chương 4: Biến ngẫu nhiên liên tục:
1. Biến ngẫu nhiên liên tục
a. Định nghĩa
Biến ngẫu nhiên liên tục (Continuous Random Variable) là biến ngẫu nhiên có thể nhận mọi giá trị trong một khoảng .Vi dụ:
•Thời gian đi từ nhà đến trường của sinh viên
• Lợi nhuận của nhà đầu tư cổ phiếu sau một năm .
•Cân nặng của trẻ sơ sinh ở Việt Nam
b. Hàm phân phối xác suất
-Hàm phân phối xác suất( hàm tích lũy xác suất - Cumulative Distribution Function) của biến ngẫu nhiên X là: F(x) = P(X < x), x R
R
-Tính chất:P(a ≤ X ≤ b) = F(b) – F(a)
c. Hàm mật độ xác suất
Cho X là biến ngẫu nhiên liên tục, hàm mật độ xác suất (Density Function) của X, ký hiệu f(x), là: f(x) = F'(x)
Tính chất hàm mật độ:
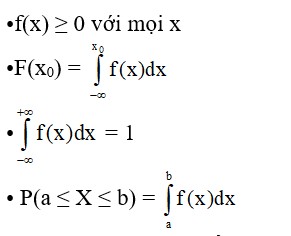
>> Thi thử trắc nghiệm miễn phí Xác suất thống kê
2. Quy luật phân phối xác suất
a. Quy luật phân phối xác suất Chuẩn(Quan trọng)
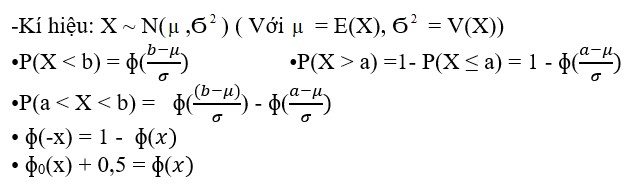
Ví dụ về bài tập công thức xác suất đầy đủ,công thức Bayes trong đề thi giữa kỳ(Có thể sẽ là câu khó nhất đề):
Bài 5: (ĐỀ CÔ HUYỀN)Một nhà máy có tỷ lệ phế phẩm là 8%.Các sản phẩm sản xuất ra được đi qua một mấy kiểm tra chất lượng tự động. Máy kiểm tra có tỷ lệ sai sót khi kiểm tra chính phẩm là 2%,tỷ lệ sai sót khi kiểm tra phế phẩm 1%.Tìm tỉ lệ sản phẩm máy kiểm tra tự động kết luận là phế phẩm là?
Giải:
Chẩn bệnh: Sinh viên thường rất ngại hoặc cảm thấy sợ hãi khi gặp phải những bài tập như thế này vì:
-Thứ nhất: Đề bài thường rất lằng nhằng, phức tạp, đọc xong không biết mình phải tính cái gì và phải làm cái gì?
-Thứ hai: Cho dù biết là phải dùng công thức xác suất đầy đủ nhưng không biết phải tính như thế nào?, bắt đầu ở đâu?, đặt tên biến cố là gì?
-Thứ ba: Đầu bài có nhiều “ngôn từ gây lú” như là: “lấy 2 sản phẩm từ hộp 1 bỏ sang hộp 2 rồi từ hộp 2 lấy ra 2 sản phẩm…”; “Máy kiểm tra có tỷ lệ sai sót khi kiểm tra chính phẩm là 2%”; “tỷ lệ sai sót khi kiểm tra phế phẩm 1%”; vân vân và mây mây…. Dẫn đến việc cái bạn đọc đề xong tư duy bị lẫn lộn, ức chế, rồi thì áp lực về thời gian, điểm số đầu óc không nghĩ được gì nữa khiến cho các bạn nản và bỏ cuộc
Chữa bệnh: Phác đồ điều trị như sau:

Áp dụng cụ thể vào bài này
Bài 5: (ĐỀ CÔ HUYỀN)Một nhà máy có tỷ lệ phế phẩm là 8%.Các sản phẩm sản xuất ra được đi qua một máy kiểm tra chất lượng tự động. Máy kiểm tra có tỷ lệ sai sót khi kiểm tra chính phẩm là 2%,tỷ lệ sai sót khi kiểm tra phế phẩm 1%.Tìm tỉ lệ sản phẩm máy kiểm tra tự động kết luận là phế phẩm là?
Bước 1: Xác định nhóm các biến cố đấy đủ, đặt tên biến cố:
Lấy một sản phẩm thì sẽ có 2 trường hợp:Một là lấy được chính phẩm và hai là lấy được phế phẩm.(Đây chính là nhóm BCĐĐ)

Hãy ôn tập thật hiệu quả và chúc các bạn đạt kết quả tốt trong bài kiểm tra sắp tới!

Để các bạn có được sự chuẩn bị tốt nhất cho bài thi giữa kỳ cho môn học này, mình sẽ hệ thống lại kiến thức từ chương 1 tới chương 4 để các bạn có thể dễ dàng hơn trong việc ôn tập và đạt điểm cao.
Chờ gì nữa, bắt đầu thôi !!
I. Chương 1: Chương mở đầu
Chương này chỉ mang tính chất giới thiệu,bạn nào muốn đọc thì đọc, không muốn thì có thể bỏ qua nhé ^^
II. Chương 2: Biến cố và xác suất
Chương này cần nhớ các công thức xác suất biến cố tổng, biến cố tính,xác suất đầy đủ,công thức Bayes,công thức Bernoulli…
Xác suất của biến cố tích
• Với A và B là 2 biến cố độc lập ta có: P(AB) = P(A).P(B)
• Với A và B là 2 biến cố phụ thuộc ta có: P(AB) = P(A/B).P(B) = P(B/A).P(A)
•Với A và B là 2 biến cố xung khắc ta có: P(AB) = 0
Xác suất của biến cố tổng

-Giả sử có n phép thử độc lập
-Trong mỗi phép thử,xác suất để xảy ra biến cố A là như nhau và bằng p, xác suất không xảy ra A là 1 – p
-Xác suất để trong n phép thử đó, biến cố A xảy ra đúng x lần được ký hiệu là P(x | n,p)
-Công thức Bernoulli:
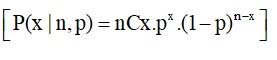
Công thức XS đầy đủ,công thức Bayes
- Cho H1, H2,….., Hn là một nhóm đầy đủ các biến cố

>> Hiểu rõ Xác suất thống kê hơn cùng mentor Viết Duy !!
III. Chương 3: Biến ngẫu nhiên rời rạc
1) Khái niệm:
• Kí hiệu biến ngẫu nhiên: X,Y, Z,.. Giá trị có thể có của X ký hiệu: X1, X2, Xn .
-Một biến được gọi là biến ngẫu nhiên rời rạc nếu các giá trị có thể có của nó lập nên một tập hợp hữu hạn hoặc đếm được.
2) Bảng phân phối xác suất(Chỉ BNN rời rạc mới có)
•Cho biến NN rời rạc X nhận các giá trị x1,x2,…,xn với xác suất tương ứng p1,p2,…pn.
| X | x1 | x2 | ………. | xk | ………. | xn |
| P | p1 | p2 | ……….. | pk | ………… | pn |
Bảng trên gọi là bảng phân phối xác suất của biến ngẫu nhiên rời rạc X
3)Các tham số đặc trưng
•Kì vọng(trung bình)
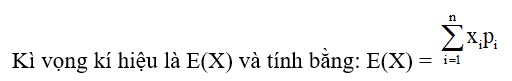
Đơn vị của kì vọng là đơn vị của X
Tính chất:

•Phương sai:
-Phương sai phản ảnh độ phân tản của biển ngẫu nhiên. Phương sai lớn thì độ phân tán lớn. Phương sai phản ánh độ rúi ro, độ ổn định, độ đồng đều.

4) Quy luật Phân phối xác suất cho BNN rời rạc
•Quy luật phân phối 0 – 1
Định nghĩa: Biến ngẫu nhiên rời rạc X chỉ nhận một trong hai giá trị hoặc 1 với xác suất được tính bởi công thức
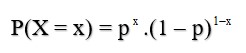
Được gọi là có phân phối 0- 1 với tham số p. Kí hiệu: X ~ A(p)
X có bảng phân phối xác suất
| X | 0 | 1 |
| P | 1 – p | P |
Tham số đặc trưng: E(X) = p: V(X) = p(1 – p)
•Quy luật phân phối Nhị thức
- Xét n phép thử độc lập. Xác suất xảy ra biến cố A trong mỗi phép thử là p. Gọi X là số lần bc A xảy ra,trong n lần thử. X có thể nhận các giá trị 0, 1, 2,..n với các xác suất tương ứng được tính theo công thức

-Các tham số đặc trưng:
• Kỳ vọng E(X) = np • Phương sai V(X) = np(1-p)
• Mốt m0: np + p -1 ≤ m0 ≤ np + p

•PHÂN PHỐI POISSON
Định nghĩa: Biến ngẫu nhiên rời rạc X nhận một trong các giá trị có thể có là 0, 1, 2, .. với các xác suất tương ứng được tính theo công thức :
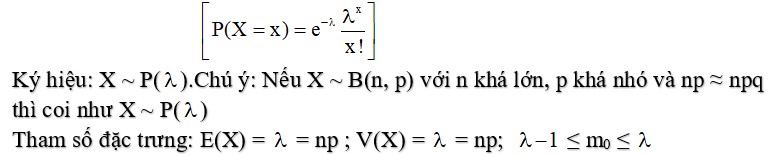
>> Thi thử ngay với bộ ngân hàng đề 1000 câu hỏi
IV. Chương 4: Biến ngẫu nhiên liên tục:
1. Biến ngẫu nhiên liên tục
a. Định nghĩa
Biến ngẫu nhiên liên tục (Continuous Random Variable) là biến ngẫu nhiên có thể nhận mọi giá trị trong một khoảng .Vi dụ:
•Thời gian đi từ nhà đến trường của sinh viên
• Lợi nhuận của nhà đầu tư cổ phiếu sau một năm .
•Cân nặng của trẻ sơ sinh ở Việt Nam
b. Hàm phân phối xác suất
-Hàm phân phối xác suất( hàm tích lũy xác suất - Cumulative Distribution Function) của biến ngẫu nhiên X là: F(x) = P(X < x), x
-Tính chất:P(a ≤ X ≤ b) = F(b) – F(a)
c. Hàm mật độ xác suất
Cho X là biến ngẫu nhiên liên tục, hàm mật độ xác suất (Density Function) của X, ký hiệu f(x), là: f(x) = F'(x)
Tính chất hàm mật độ:
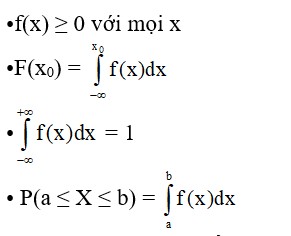
>> Thi thử trắc nghiệm miễn phí Xác suất thống kê
2. Quy luật phân phối xác suất
a. Quy luật phân phối xác suất Chuẩn(Quan trọng)
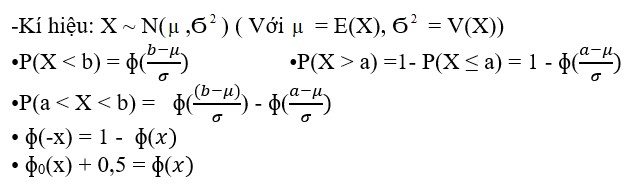
Ví dụ về bài tập công thức xác suất đầy đủ,công thức Bayes trong đề thi giữa kỳ(Có thể sẽ là câu khó nhất đề):
Bài 5: (ĐỀ CÔ HUYỀN)Một nhà máy có tỷ lệ phế phẩm là 8%.Các sản phẩm sản xuất ra được đi qua một mấy kiểm tra chất lượng tự động. Máy kiểm tra có tỷ lệ sai sót khi kiểm tra chính phẩm là 2%,tỷ lệ sai sót khi kiểm tra phế phẩm 1%.Tìm tỉ lệ sản phẩm máy kiểm tra tự động kết luận là phế phẩm là?
Giải:
Chẩn bệnh: Sinh viên thường rất ngại hoặc cảm thấy sợ hãi khi gặp phải những bài tập như thế này vì:
-Thứ nhất: Đề bài thường rất lằng nhằng, phức tạp, đọc xong không biết mình phải tính cái gì và phải làm cái gì?
-Thứ hai: Cho dù biết là phải dùng công thức xác suất đầy đủ nhưng không biết phải tính như thế nào?, bắt đầu ở đâu?, đặt tên biến cố là gì?
-Thứ ba: Đầu bài có nhiều “ngôn từ gây lú” như là: “lấy 2 sản phẩm từ hộp 1 bỏ sang hộp 2 rồi từ hộp 2 lấy ra 2 sản phẩm…”; “Máy kiểm tra có tỷ lệ sai sót khi kiểm tra chính phẩm là 2%”; “tỷ lệ sai sót khi kiểm tra phế phẩm 1%”; vân vân và mây mây…. Dẫn đến việc cái bạn đọc đề xong tư duy bị lẫn lộn, ức chế, rồi thì áp lực về thời gian, điểm số đầu óc không nghĩ được gì nữa khiến cho các bạn nản và bỏ cuộc
Chữa bệnh: Phác đồ điều trị như sau:

Áp dụng cụ thể vào bài này
Bài 5: (ĐỀ CÔ HUYỀN)Một nhà máy có tỷ lệ phế phẩm là 8%.Các sản phẩm sản xuất ra được đi qua một máy kiểm tra chất lượng tự động. Máy kiểm tra có tỷ lệ sai sót khi kiểm tra chính phẩm là 2%,tỷ lệ sai sót khi kiểm tra phế phẩm 1%.Tìm tỉ lệ sản phẩm máy kiểm tra tự động kết luận là phế phẩm là?
Bước 1: Xác định nhóm các biến cố đấy đủ, đặt tên biến cố:
Lấy một sản phẩm thì sẽ có 2 trường hợp:Một là lấy được chính phẩm và hai là lấy được phế phẩm.(Đây chính là nhóm BCĐĐ)

Hãy ôn tập thật hiệu quả và chúc các bạn đạt kết quả tốt trong bài kiểm tra sắp tới!